Sampling Theorem Formula 1-D:
One of the most important applications of digital filtering is the processing of sequences of samples derived from continuous or analog signals. This is made possible due to the results and implications of the Sampling Theorem Formula.
This theorem can be stated as follows:
“A continuous analogue function x(t) which has a limited Fourier spectrum, that is a spectrum x(jω) such that x(jω) = 0 for ω > ωm, is uniquely described from a knowledge of its values at uniformly spaced time instants T units apart, where T = 2π/ωs, and ωs ≥ 2ωm“.
Sampling Theorem 2-D:
This theorem can be stated as follows.
A function of two variables, x(x1, x2) whose 2-D Fourier transform is equal to zero for ω1 > ω1m and ω2 > ω2m, is uniquely determined by the values taken at uniformly spaced points in the x1 and x2 plane, if the spacing X1 and X2 satisfy the conditions x1 ≤ π/ω1m and x2 ≤ π/ω2m.
1-D Z-Transform:
Given a sequence { x(n)} with -∞ ≤ n ≤ ∞, its Z-transform is defined as
 where Z is a complex variable.
where Z is a complex variable.
The Z-transform can be inverted and x(n) can be obtained as
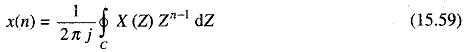 where C is the counter clockwise closed contour in the region of convergence of X(Z) and encircling the origin of the Z-plane.
where C is the counter clockwise closed contour in the region of convergence of X(Z) and encircling the origin of the Z-plane.
