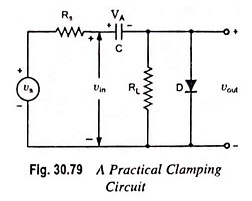
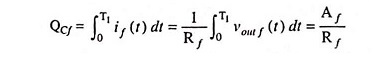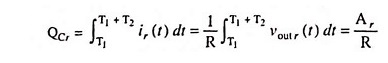Clamping Circuit Theorem:

Under steady-state conditions, for any input waveform, the shape of the output waveform of a clamping circuit is fixed and also the area in the forward direction and the area in the reverse direction are related. According to clamping circuit theorem, under steady-state conditions, the ratio of area in forward direction A_f to that of reverse direction A_r of output voltage is equal to the ratio of diode forward resistance R_f to resistance R connected across diode.

This theorem applies quite generally independent of the input waveform and the magnitude of the source resistance.

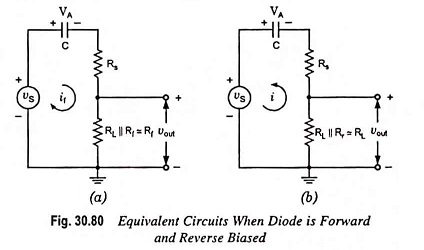
Proof: Consider the clamping circuit shown in Fig. 30.79. Let for first half cycle of input signal diode be on, the equivalent circuit is shown in Fig. 30.80 (a). If v_{out f}(t) is the output waveform in the forward direction, then the capacitor charging current is

Therefore, the charge stored in the capacitor during the forward interval is

Similarly for interval T₁ < t <T₁ + T₂, the input is low and the diode is off and the equivalent circuit is as shown in Fig. 30.80 (b). If v_{out r}(t) is the output voltage in the reverse direction, then the discharging current of capacitor is

Thus, the charge lost by the capacitor during the reversal interval is

Under steady-state conditions, the net charge gain of the capacitor over one complete cycle must be equal to zero, therefore,