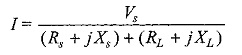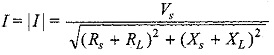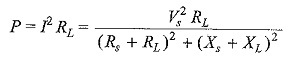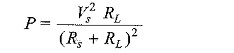Maximum Power Transfer Theorem:

Here, the maximum power transfer theorem has been discussed for resistive loads. The maximum power transfer theorem states that the maximum power is delivered from a source to its load when the load resistance is equal to the source resistance. It is for this reason that the ability to obtain impedance matching between circuits is so important.

For example, the audio output transformer must match the high impedance of the audio power amplifier output to the low input impedance of the speaker. Maximum Power Transfer is not always desirable, since the transfer occurs at a 50 per cent efficiency.

In many situations, a maximum voltage transfer is desired which means that unmatched impedances are necessary. If maximum power transfer is required, the load resistance should equal the given source resistance. The maximum power transfer theorem can be applied to complex impedance circuits. If the source impedance is complex, then the maximum power transfer occurs when the load impedance is the complex conjugate of the source impedance

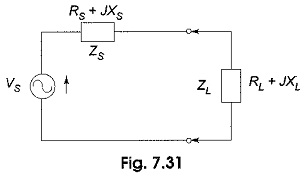
Consider the circuit shown in Fig. 7.31, consisting of a source impedance delivering power to a complex load.

Current passing through the circuit shown

Magnitude of current

Power delivered to the circuit is

In the above equation, if R_L is fixed, the value of P is maximum when

Then the power

Let us assume that R_L is variable. In this case, the maximum power is transferred when the load resistance is equal to the source resistance. If R_L = R_s and X_L = -X_s, then Z_L = Z^*_s. This means that the Maximum Power Transfer occurs when the load impedance is equal to the complex conjugate of source impedance Z_s.