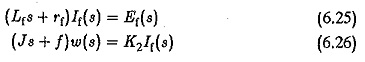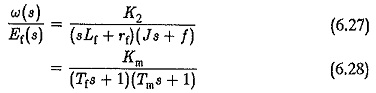Transfer Function of a Field Controlled DC Motor:

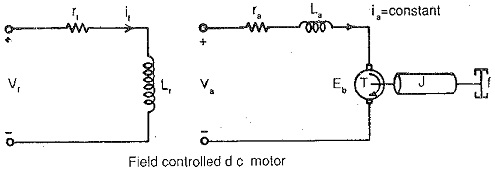
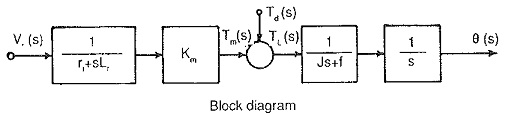
The speed of a dc motor can be varied by varying the field current. The speed can be increased beyond base speed by decreasing the field current. The Fig. 6.8(c&d) shows the Transfer Function of a Field Controlled DC Motor. In this type of control constant torque operation is not possible as the armature current would increase to dangerous values at low fluxes. It is therefore necessary to maintain the armature current at a constant value at all flux levels. The field current is varied. The armature is also supplied by means of a phase controlled rectifier to maintain constant armature current. While deriving the transfer function the effects of saturation and armature reaction are neglected.

The torque developed by the motor

In a Transfer Function of a Field Controlled DC Motor as discussed above, the armature current is constant and field current is variable. Therefore we have

The equation of the Transfer Function of a Field Controlled DC Motor is given by

The dynamic equation of the motor is

The Laplace transforms of Eqs 6.22 — 6.24 with zero initial conditions are given by

Eliminating I_t(s) from Eq. 6.26 and simplifying we get

where

K_m = K₂/(r_f.f) motor gain constant

T_f = L_f/r_f field time constant

T_m = J/f mechanical time constant.

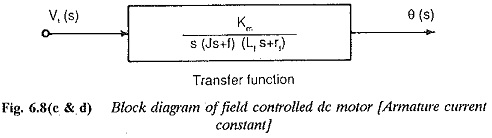
Since the field inductance cannot be neglected, Transfer Function of a Field Controlled DC Motor hav­ing speed as variable quantity is a second order system. The block diagram of the system and its transfer function are shown in Fig 6.8(d).

Comparison of Armature Controlled and Field Controlled DC Motors: