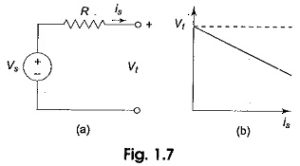
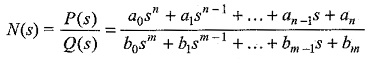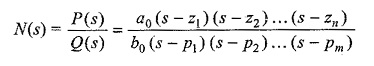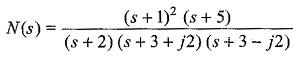Poles and Zeros of Transfer Function:

Poles and Zeros of Transfer Function defines that, in general, the network function N(s) may be written as

where a₀,a₁,…a₂ and b₀,b₁,…b_m are the coefficients of the polynomials P(s) and Q(s); they are real and positive for a passive network. If the numerator and denominator of polynomial N(s) are factorized, the network function can be written as

where z₁,z₂,…z_n are the n roots for P(s)= 0

and p₁,p₂,…p_m are the m roots for Q(s) = 0

and a₀/b₀ = H is a constant called the scale factor.

z₁,z₂,…z_n in the transfer function are called zeros, and are denoted by 0. Similarly, p₁,p₂,…p_m are called poles, and are denoted by x. The network function N(s) becomes zero whens is equal to anyone of the zeros. N(s) becomes infinite when s is equal to any one of the poles. The network function is completely defined by its Poles and Zeros of Transfer Function. If the poles or zeros are not repeated, then the function is said to be having simple poles or simple zeros. If the poles or zeros are repeated, then the function is said to be having multiple poles multiple zeros. When n > m, then (n — m) zeros are at s = ∞, and for m > n, (m — n) poles are at s = ∞.

Consider, the network function

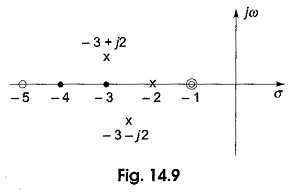
that has double zeros at s = – 1 and a zero at s = – 5; and three finite poles at s = – 2, s = – 3 + j2, and s = – 3 – j2 as shown in Fig. 14.9.

The network function is said to be stable when the real parts of the poles and zeros are negative. Otherwise, the poles and zeros must lie within the left half of the s-plane.