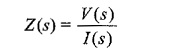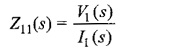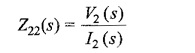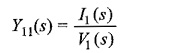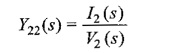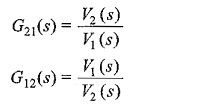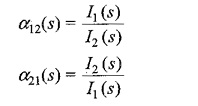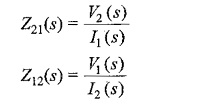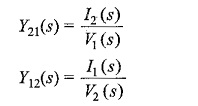Transfer Function of Two Port Network:
For a one-port network, the driving point impedance or impedance of the network is defined as
The reciprocal of the impedance function is the driving point admittance function, and is denoted by Y(s).
For the Transfer Function of Two Port Network without internal sources, the driving point impedance function at port 1-1′ is the ratio of the transform voltage at port 1-1′ to the transform current at the same port.
Similarly, the driving point impedance at port 2-2′ is the ratio of transform voltage at port 2-2′ to the transform current at the same port.
For the Transfer Function of Two Port Network, the driving point admittance is defined as the ratio of the transform current at any port to the transform voltage at the same port.
Therefore
or
Which is the driving point admittance.
The four other network functions are called transfer functions. These functions give the relation between voltage or current at one port to the voltage or current at the other port as shown here under.
(i) Voltage transfer ratio:
This is the ratio of voltage transform at one port to the voltage transform at the other port, and is denoted by G(s)
(ii) Current transfer ratio:
This is the ratio of current transform at one port to current transform at other port, and is denoted by α(s)
(iii) Transfer impedance:
It is defined as the ratio of voltage transform at one port to the current transform at the other port, and is denoted by Z(s).
(iv) Transfer admittance:
It is defined as the ratio of current transform at one port to the current transform at the other port, and is denoted by Y(s).
The above network functions are found by forming the system of equations using node or mesh analysis, and taking the transforms of equations by setting the initial conditions to zero and solving for ratio of the response to excitation.