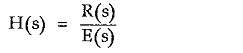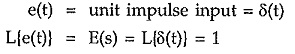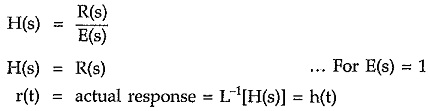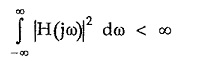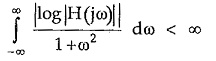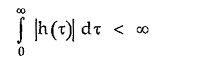Realisability of One Port Network:
Realisability of One Port Network – Consider the network function H(s) which is the ratio of Laplace transform of the output R(s) to the Laplace transform of the excitation E(s).
In the synthesis, we are going to obtain a network from the given network function which may be admittance function or impedance function. But before synthesizing H(s), it is necessary to check whether H(s) is physically realizable or not, using passive elements. For this, there are two important conditions related to a network which are causality and stability.
Now there can not be output without input i.e. there can not be current without any voltage. So there exists a cause and effect relationship between input and output. This is nothing but causality. To have the given One Port Network to be causal, the impulse response of the network must be zero for t<0. The impulse response means the response of the network to the unit impulse input.
The Laplace transform of unit impulse function is always unity.
Thus unit impulse response of the network is inverse Laplace transform of the network function. For a network to be causal the condition is,
Impulse response = h(t) = 0, for t<0
This is the required condition for the network to be causal. Thus the impulse response h(t) = e-2t u(t) is causal as u(t) = 0 for t< 0 thus h(t) is also zero for t<0.
While the response like h(t) = e-2|t| is not causal.
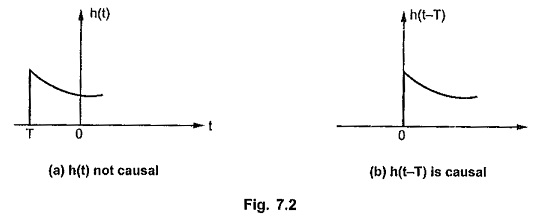
Practically in certain cases, the impulse response can be made causal by delaying it. Consider the response h(t) shown in the Fig. 7.2 (a). It is not causal. But delaying it by T, it becomes zero for all t< 0 and hence becomes causal. This is shown in the Fig. 9.2 (b).
If the response is delayed by T then it becomes causal and realizable. For a system function to be causal in frequency domain, it must satisfy the condition that h(t) must possess a Fourier transform H(jω) and the square magnitude function |H(jω)|2 must be integrable i.e.,
If the system function is to be causal then it must satisfy the condition in frequency domain called Paley-Wiener criterion. The criterion states that it is necessary and sufficient condition for an amplitude function |H(jω)| to be causal that
This means that the amplitude |H(jω)|of a realizable i.e. causal network must not be zero over a finite band of frequencies.
Similar to causality, the network must be checked for stability. The One Port Network is said to be stable if,
- It produces a bounded output for a bounded input.
- There is no output if input is reduced to zero.
Thus if e(t) is the excitation and |e(t)| < k1 for 0 ≤ t ≤ ∞ then output r(t) must satisfy |r(t)| < k2 for 0 ≤ t ≤ ∞.
The k2 and k2 are real, positive, finite constants.
The stable network must satisfy the condition that its impulse response must be absolutely integrable.
This gets satisfied when the impulse response h(t) approaches zero as t approaches infinity,
In general for a stable network, the impulse response must be bounded for all t i.e.![]()
where K is positive, real, finite number.
Now the functions like sin(ωt) and cos(ωt) are bounded but are not absolutely integrable. Such systems have poles on the imaginary axis. These systems are not stable from integration definition but stable from bounded definition. Hence such systems are called marginally stable systems.
For the stability of network function H(s), it must satisfy following conditions,
- H(s) should not have a pole in right half of s-plane.
- The poles of H(s) on the imaginary axis must be nonrepeated. There should not be multiple poles of H(s) on imaginary axis.
- The degree of the numerator of H(s) can not exceed the degree of the denominator by more than unity.
Thus first step in the synthesis is to obtain the information whether the given function is realizable or not. For a given function to be realizable it is essential that the One Port Network function should satisfy all the properties of Hurwitz polynomials and those of positive real functions. Hence before the study of actual synthesis, it is necessary to study the properties of Hurwitz polynomials and the positive real functions.