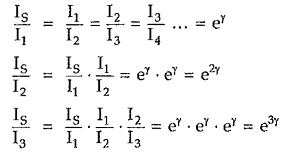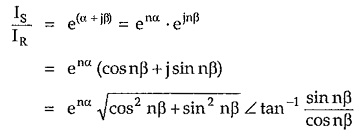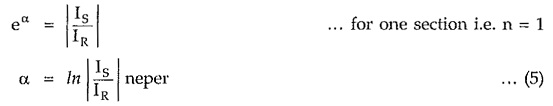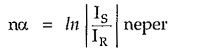Symmetrical Network in Network Analysis:
A symmetrical network has two important properties as
- Characteristic impedance (Z0)
- Propagation constant (γ)
The two networks having the same electrical properties i.e. characteristic impedance (Z0) and propagation constant (γ) are called equivalent networks or identical networks.
Characteristic Impedance (Z0):
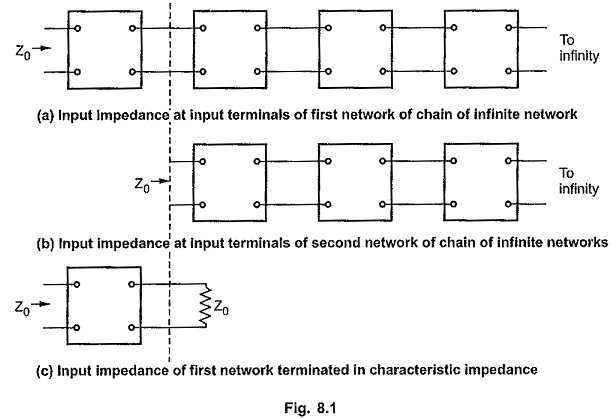
Consider that infinite number of identical symmetrical networks are connected in cascade or tandem as shown in the Fig. 8.1 (a). The input impedance measured at the input terminals of the first network in the chain of infinite networks will have some finite value which depends on the network composition. This impedance is the important property of a symmetrical network. Thus the characteristic impedance of a symmetrical network is the impedance measured at the input terminals of the first network in the chain of infinite networks in cascade and it is represented by Z0.
If first network is disconnected from the chain as shown in the Fig. 8.1 (b), then also the input impedance measured at the input terminals of second network will be Z0 again as number of networks in the chain are still infinite. That means we can replace this chain by impedance Z0 at the output port of the first network as shown in the Fig. 8.1 (c). Then the impedance at input terminals of the first network will be still Z0.
Thus in general when any symmetrical network is terminated in its characteristic impedance Z0, the input impedance will also be Z0.
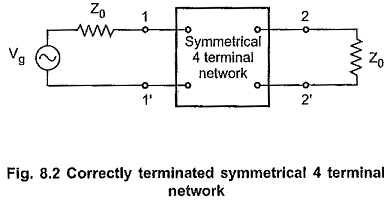
This property is true for output impedance if the symmetrical network terminated in Z0 is driven by a generator with internal impedance equal to Z0. In such network, the output impedance will be Z0 only. The network terminated in characteristic impedance at input as well as output terminals is said to be correctly terminated or properly terminated symmetrical network as shown in the Fig. 8.2.
Propagation Constant (γ):
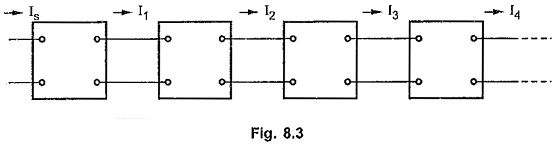
Consider a chain of identical symmetrical networks connected in cascade as shown in the Fig. 8.3.
The current leaving any section will be definite proportion of that entering section and in general will be out of phase with it. Thus the relationship between the currents entering and leaving the section is a vector quantity with both modulus and angle. This quantity is represented in the form eγ for convinence where γ is a complex number given by γ = α + jβ
Let the ratio of input to output current be given by
Since all the sections are identical, we can write
Hence for n identical sections connected is cascade the ratio of input to output current is given by
Note that input current is represented by sending end current, IS; while the output current is represented by receiving end current, IR. Above equation can be written as
when enα gives ratio of absolute magnitudes of sending end current to receiving end current and nβ gives the phase angle between these two currents.
If the network is correctly terminated, then we can write,
The real part α of the propagation constant γ is called attenuation constant and it is measured in nepers.
Similarly for n-sections,
The imaginary part β of propagation constant γ is called phase constant and is equal to the angle in radians by which output current leaving section lags that input current entering section. For n-sections, the phase constant will be nβ radians.