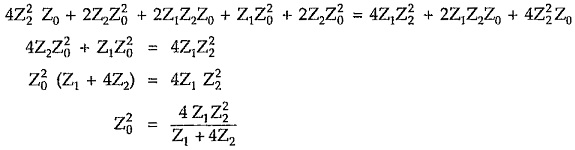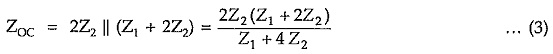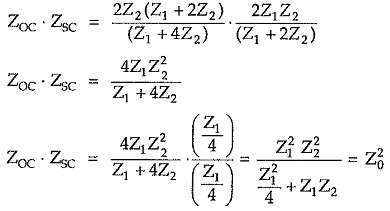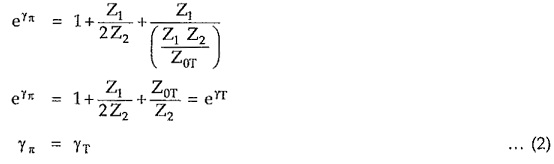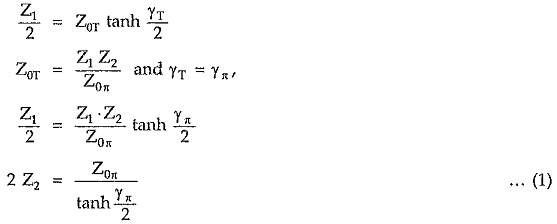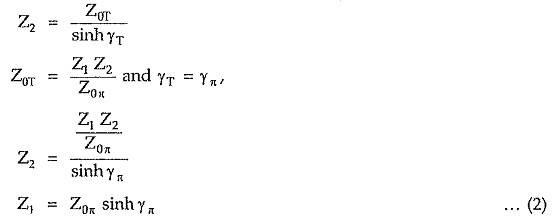Symmetrical pi Network in Network Analysis:

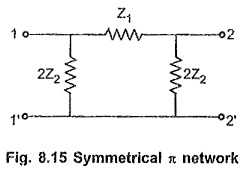
The Symmetrical pi Network in Network Analysis is another important network in line transmission fulfilling the conditions of total series and shunt arm impedances as Z₁ and Z₂ respectively. Thus the series arm impedance of a it network is selected as Z₁ and to have a total shunt arm impedance of Z₂, each shunt arm impedance is selected as 2Z₂ as shown in the Fig. 8.15.

Similar to the symmetrical T network, let us derive the expressions for the characteristic impedance (Z₀) and propagation constant (γ) of the Symmetrical pi Network in Network Analysis.

Characteristic Impedance (Z₀):

(A) In terms of series and shunt arm impedances

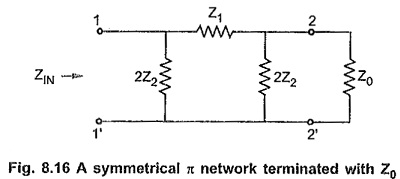
Consider a symmetrical π network terminated at its output terminals with its characteristic impedance Z₀ as shown in the Fig. 8.16.

By the property of the symmetrical network, the input impedance of such network terminated with Z₀ at other port is equal to Z₀.

The input impedance of a symmetrical π network is given by

Multiplying numerator and denominator by the factor Z₁/4,

Here the characteristic impedance of it section is indicated by Z_0π and that of T section by Z_0T.

Taking square root on both the sides,

(B) In terms of open and short circuit impedances

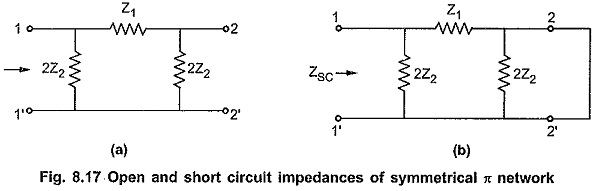
Consider Symmetrical pi Network in Network Analysis shown in the Fig. 8.17 (a) and Fig. 8.17 (b).

Consider Fig. 8.17 (a),

Consider Fig. 8.17 (b),

Multiplying equations (3) and (4), we can write,

Thus the characteristic impedance of symmetrical π network is given by

Propagation Constant (γ):

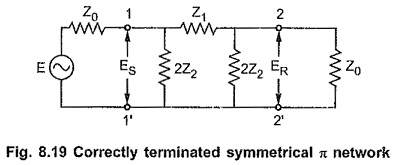
Consider correctly terminated symmetrical π network as shown in the Fig. 8.19.

As the network is symmetrical, by definition,

By potential divider rule,

Rearranging the terms,

where γ_π is the propagation constant of symmetrical π network. Putting value of Z_0π interms of Z_0T,

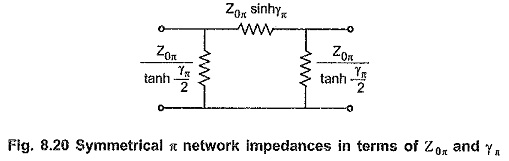
Series and shunt arm impedances of symmetrical π network in terms of Z_0π and γ_π:

For symmetrical T network, each series arm is given by,

Similarly shunt arm of symmetrical T network is given by

Hence π network with series and shunt arms expressed in terms of Z_0π and γ_π, is as shown in the Fig. 8.20.