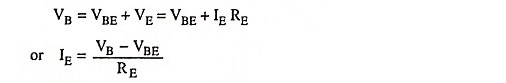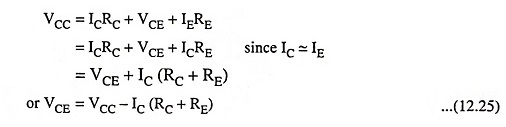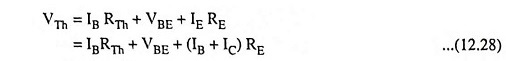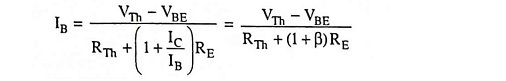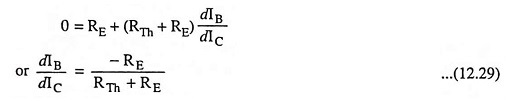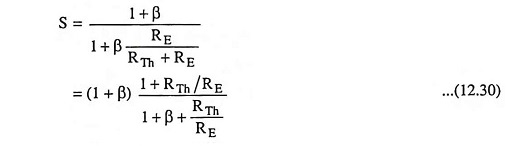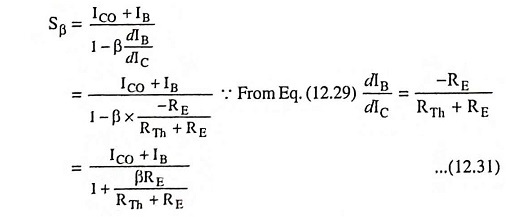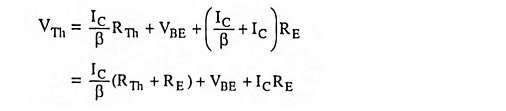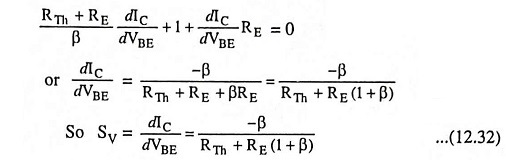Self Bias or Potential Divider Bias Circuit:

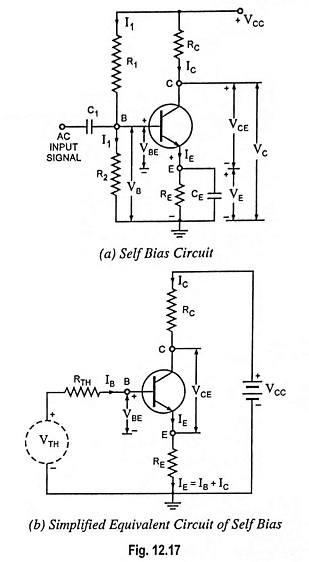
This is the most commonly used biasing arrangement. The arrangement of Self Bias or Potential Divider Bias Circuit is shown in Fig. 12.17 (a). The name voltage divider is derived due to the fact that the voltage divider is formed by the resistors R₁ and R₂ across V_CC. The emitter resistor R_E provides stabilization. The resistor R_E causes a voltage drop in a direction so as to reverse bias the emitter junction. Since the emitter-base junction is to be forward biased, the base voltage is obtained from supply V_CC through R₁ – R₂ network.

For forward biasing the emitter-base junction R₁ and R₂ are so adjusted that the base terminal becomes more positive than emitter. The net forward bias across the emitter-base junction, V_BE is equal to V_B minus dc voltage drop across R_E. The dc bias circuit is independent of transistor current gain factor β. In case of amplifiers, to avoid the loss of ac signal (because of feedback caused by R_E) a capacitor of large capacitance is connected across R_E. The capacitor offers a very small reactance to the ac signal and so it passes through the capacitor.

Approximate Circuit Analysis:

Voltage divider bias circuits are usually designed to have the voltage divider current very much larger than the transistor base current I_B and in this circumstance, base voltage V_B is largely unaffected by base current I_B and therefore, V_B can be assumed to remain constant.

Assuming the current flowing through the resistor R₁ to be equal to I₁ and neglecting base current I_B, being much smaller than voltage divider current, current flowing through resistance R₂ can also be assumed to be equal to I₁

Voltage across resistance R₂,

Applying Kirchhoff’s second (or voltage) law to the base-emitter loop [Fig. 12.17(a)] we have

and collector current,

Applying Kirchhoff’s second (or voltage) law to the collector-emitter loop we have

From Eqs. (12.24) and (12.25) the values of I_C and V_CE can be determined and the quiescent point Q is established.

It is clear from Eq. (12.24) that I_C does not at all depend upon β. Though collector current l_C depends upon V_BE but in practice V_BE is very small in comparison to V_B and so collector current I_C is practically independent of V_BE. Thus collector current I_C in this biasing circuit is almost independent of transistor parameters and hence good stabilization is ensured.

In this Potential Divider Bias Circuit the emitter resistance R_E provides excellent stabilisation. This is explained as below :

Now let the temperature of transistor junction rise when it is loaded. This causes increase in leakage currents and so increase in the value of β. Hence collector current I_C tends to increase. With the increase in the value of l_C, voltage drop across emitter resistance R_E increases. Since voltage drop across R₂ (i.e. V_B) is independent of collector current, therefore, V_BE decreases and so I_B, I_E and I_c.

Thus we see that the Potential Divider Bias Circuit has tendency to hold the Q point (I_C) stable automatically. This is due to feedback action. The increase in I_C has immediately a reaction change of feedback so as to correct the situation.

Precise Circuit Analysis:

For exact analysis of a self bias or Potential Divider Bias Circuit, the voltage divider (the circuit to the left of the base terminal) is replaced by its Thevenin’s equivalent circuit, as shown in Fig. 12.17 (b).

Open-circuit voltage across base and ground terminals,

Resistance seen into the base and ground terminals with V_CC short circuited,

Applying Kirchhoff’s voltage law around the closed base circuit [Fig. 12.17 (b)] yields

or Base current,

Once the base current has been determined, l_C can be computed using appropriate value of β, and the transistor terminal voltages can then be computed.

Stability Factor:

Differentiating Eq. (12.28) w.r.t. I_C (considering V_BE to be independent of l_C) we have

From Eq. (12.5) stability factor S is given as

Substituting the value of dI_B/dI_C from Eq. (12.29) in above equation we have

Stability factor,

The above equation shows that stability factor S varies between 1 for small values of R_Th/R_E and (1 + β) for larger values of R_Th/R_E. For proper operation both R_E and V_CC should be larger  and R_Th small. Typical practical value of S for this type of biasing circuit is about 10.

Equation (12.28) may be written as

Differentiating above equation w.r.t. V_BE, we have