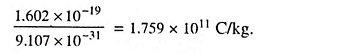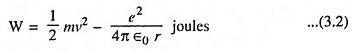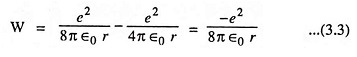Rutherford Nuclear Model of Atomic Structure:
In order to explain many phenomena associated with conduction in gases, metals and semiconductors and the electron emission from a metal surface, it is necessary to assume that the atom has loosely bound electrons which can be torn away from it. On the basis of experiments on the scattering of α-particles, combined with the discovery of neutron made by Chadwick in 1932, Rutherford suggested a complete model of the atom which is known as Rutherford Nuclear Model of Atomic Structure.
According to this model : The centre of an atom consists of a positively charged body which is called nucleus. All the protons and neutrons are present in the nucleus. Although the nucleus is small, it is heavy due to the presence of all the protons and neutrons in it. Since the mass of electron is negligible, the mass of an atom is equal to the sum of the masses of protons and neutrons, i.e., the entire mass of an atom resides in its nucleus.
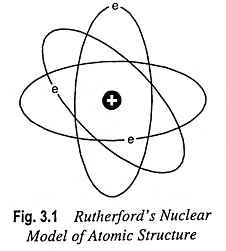
The electrons keep revolving in the orbits around the nucleus at extremely high speed and at large distance from the nucleus as the planets revolve around the Sun (Fig. 3.1). Thus Rutherford Nuclear Model of Atom is comparable to solar system and it is for this reason that the electrons revolving around the nucleus are generally referred to as planetary electrons.
Since the atom is neutral, the number of electrons which are negatively charged particles is equal to the number of protons in the nucleus or the atomic number of the atom. The electrons revolve around the nucleus with such a speed that the centrifugal force (i.e., repulsive force) acquired by the electrons due to their motion just balances the attractive force between the electrons and the nucleus.
The charge associated with each electron is 1.602 x 10-19 C. Compared to mass of nucleus, electrons are relatively tiny particles of almost negligible mass (each electron weighing 9.107 x 10-31 kg). Protons and neutrons each have mass about 1,800 times the mass of an electron.
The diameter of an atom is approximately 10-10 m and that of nucleus is about 10-15 m. The ratio of e/m for an electron is equal to
Since it is not very easy to determine either the charge or the mass of an electron, electrons are usually identified by their high ratio of charge to mass. This is so high that a number of electrons making up a mass of 1 x 10-6 kg placed 100 km from a similar mass in air would experience a force of about 3 x 109 kg. No other particle has so high a value of e/m, so that recognition by this means is easy and certain.
The number of protons (or electrons) in an atom is referred to as the atomic number (Z) of the atom. Now the term atomic number is often referred to as the proton number. The total number of protons and neutrons in the nucleus of an atom is called the mass number A, of the atom. The atomic mass (or atomic weight) is the actual weight of an atom and numerically slightly differs from the mass number of the atom. For example, aluminium has 79 protons and 118 neutrons. Thus its atomic number Z is equal to 79, being equal to the number of protons and the mass number A = 79 + 118 = 197.
The force of attraction between the electrons and nucleus follows Coulomb’s law. It can be shown from classical mechanics that the resultant closed path will be a circle or an ellipse under the action of such a force.
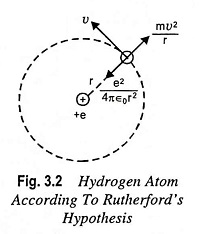
Let us consider a hydrogen atom having a single electron, revolving around the nucleus which has a single proton, in a circular orbit with radius r as depicted is Fig. 3.2.
The force of attraction between the nucleus and the electron is
where
- e = electronic charge is in coulombs
- r = separation between the two particles is in metres, the force is in newtons,
- ε0 = is the permittivity of free space and is equal to 8.854 x 10-12 F/m.
By Newton’s second law of motion, this must be equal to the product of electronic mass m in kg and the acceleration ν2/r toward the nucleus, where ν is the speed of the electron in the circular path, in m/s. Then
Furthermore, the potential energy of the electron at a distance r from the nucleus is
The kinetic energy is
Then, according to conservation of energy,
Combining Eqs. (3.1) and (3.2) we have
The above Eq. (3.3) provides the desired relationship between the radius r and the total energy of the electron. This equation also shows that the total energy of the electron is always negative. The negative sign arises because the potential energy has been chosen to be zero when r is infinite. It is also evident from above equation that the energy of the electron becomes smaller (i.e., more negative), as it approaches close to the nucleus.
Weakness of Rutherford’s Atomic Model:
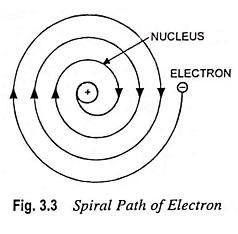
The assumptions that electrons were orbiting about the nucleus was unfortunate. According to the classical electromagnetic theory if a charged particle accelerates around an oppositely charged particle, the former will radiateenergy. If an electron radiates energy, its speed will decrease and it will go into spiral motion, finally falling into the nucleus, as shown in Fig. 3.3. This does not happen actually as then the atom would be unstable, which it is not. This was the chief weakness of Rutherford Nuclear Model of Atom.
The other weakness of Rutherford Nuclear Model of Atom was that it fails to account for the following phenomenon.
When gases under low pressure are subjected to electric discharge line spectra are produced.