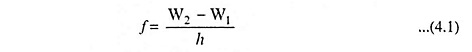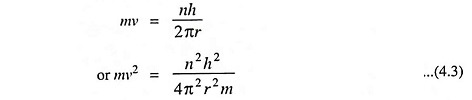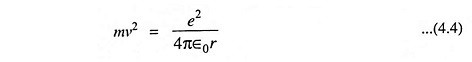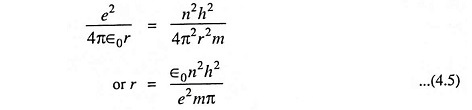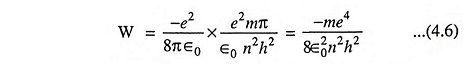Explain Bohr’s Atomic Model:
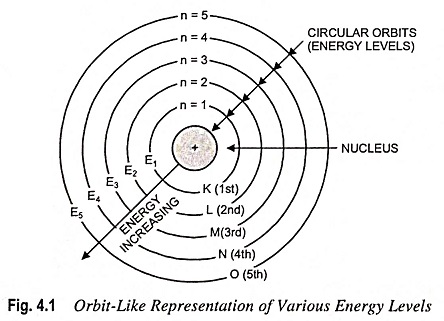
Bohr’s Atomic Model – Neils Bohr, a Danish physicist, put forward his model of atom in 1913. He retained Rutherford’s model of a very small positively charged nucleus at the centre. He also accepted the view that all the protons and neutrons (and hence most of the mass of the atom) are contained in the nucleus. He also agreed that the negatively charged electrons are revolving around the nucleus in the same way as the planets are revolving around the Sun. But he took a bold step forward by applying Planck’s quantum theory to the electrons revolving around the nucleus. He postulated the following three fundamental laws :
1. The electrons continue revolving in their respective orbits without losing energy. This is because energy in fraction of a quantum cannot be lost.
In other words, the energy of an electron remains constant as long as it stays in the same orbit. This led to the idea that each orbit is associated with a definite energy, i.e., with a definite whole number of quantas of energy. The orbits, therefore, are also known as energy levels or energy shells. Bohr’s Atomic Model gave numbers 1, 2, 3, 4, etc., (starting from the nucleus) to these energy levels, as shown in Fig. 4.1. These are now termed as principal quantum numbers. The various energy levels are also designated by letters K, L, M, N, etc. The farther the energy level from the nucleus, the greater is the energy associated with it. As long as the electron remains in a particular energy shell, it neither emits nor absorbs energy.
2. Energy is emitted or absorbed by an atom only when an electron moves from one level to another. The amount of energy emitted or absorbed is given by the difference of the energies associated with the two energy levels concerned. Thus the energy of an electron cannot change continuously. It changes only abruptly as the electron jumps from one energy level to another. The same idea has been expressed by the statement that for a change of electronic energy, the electron has to jump and not to ‘flow’ from one energy level to another.
In a transition from one stationary state corresponding to a definite energy W2 to another stationary state, with an associated energy W1 radiation will be emitted. The frequency of this radiant energy is given by
where h is Planck’s constant in joule-seconds, the W’s are expressed in joules, and f is in hertz.
3. The angular momentum of an electron moving around the nucleus is quantized. An electron, like any other body moving in a circular orbit, has an angular momentum given by mrv where m is the mass, v is the velocity of the electron while r is the radius of the orbit. Bohr’s Atomic Model postulated that these orbits or energy levels are such that the angular momentum can have only definite or discrete values given by the expression
where n is an integer (1, 2, 3, etc.).
Thus the angular momentum of an electron may be h/2π or simple whole number multiples of h/2π such as 2h/2π, 3h/2π, … nh/2π.
This principle is known as quantisation of angular momentum.
The energy level in joules of each state can be determined as follows:
From Eq. (4.2) we gave
Again from Eq. (3.1), we have
Comparing Eqs. (4.3) and (4.4), we have
The above Eq. (4.5) gives the expression for the radius of the orbit. Substituting the value of r from Eq. (4.5) in Eq. (3.3) we have