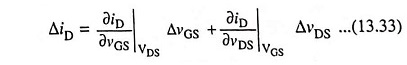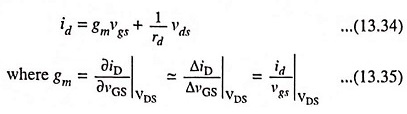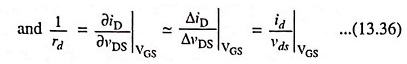Small Signal Model of FET:

The Small Signal Model of FET which consists of Low Frequency Small Signal Model for FET and High Frequency Model for FET.

Low Frequency Model: In a FET, instantaneous drain current i_D is a function of the instantaneous gate-source voltage v_GS and instantaneous drain-source voltage v_DS and is, therefore, expressed as

If both the gate and drain voltages are varied, the change in drain current is given approximately by the first two terms in the Taylor’s series expansion of Eq. (13.32) or

Using the conventional small signal notations, Δi_D, Δv_GS and Δv_DS may be replaced respectively by time varying components i_d, v_gs and v_ds. Now Eq. (13.33) becomes

Parameter g_m is the mutual conductance, or transconductance

The reciprocal of r_d is the drain conductance g_d.

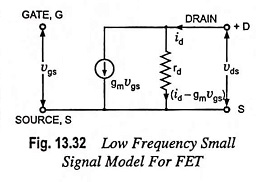
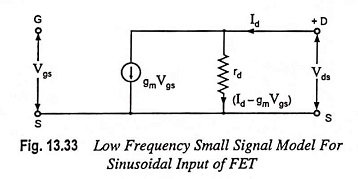
Circuit shown in Fig. 13.32 is made satisfying Eq. (13.34) giving the incremental drain current i_d in form of g_m, r_d, v_gs and v_ds. This circuit forms the low frequency Small Signal Model of FET: This model consists of one dependent current generator whose current g_mv_gs is proportional to the time varying gate source voltage v_gs and proportionality constant is the transconductance g_m.

The arrow points from drain to source to indicate a phase change of 180° (or phase reversal) between output and input voltages as will occur in actual operation. In low frequency model, as the gate is reverse biased, the gate current becomes zero. So, in low frequency model, gate to source junction is represented by an open circuit and no current is drawn by the input terminal of the FET. The reason is that input resistance, (gate-to-source resistance) is very large. The output resistance is represented by the resistance r_d (resistance from drain to source). If r_d is suffi­ciently large as compared to those of other circuit ele­ments, this is ignored. Now the equivalent circuit be­comes simply a current source whose magnitude is controlled by v_gs and g_m—clearly a voltage con­trolled current source.

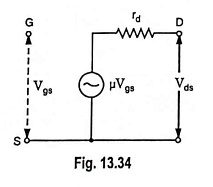
Small Signal Model of FET for sinusoi­dal input voltage of rms value V_gs may be drawn, as shown in Fig. 13.33 where v_gs, i_d, v_ds have been replaced respectively by rms values V_gs, I_d and V_ds. The voltage-controlled current source (g_m V_gs) can be replaced by equivalent volt­age-controlled voltage source (μV_gs) as depicted in Fig. 13.34.

Now the equivalent circuit consists of a voltage source (μV_gs) in series with a drain resistance r_d. Here μ is the amplification factor of the FET and is equal to the product of transconductance g_m and drain resistance r_d i.e., μ = g_mr_d.

Comparison of Low Frequency Models of FET and BJT:

1. Both FET and BJT models have a dependent current generator in the output circuit.
2. In FET models, the generator current is proportional to the input voltage V_gs while in BJT models, the generator current is proportional to the input current.
3. In FET models input impedance is very high (theoretically infinite at low frequencies) while in common emitter BJT model the input impedance is of the order of 800 Ω.
4. In FET, there is no feedback from output (drain) to the input (source) while in BJT models it is. Thus it can be safely said that at low frequencies, FET forms a more ideal amplifier than BJT amplifier.

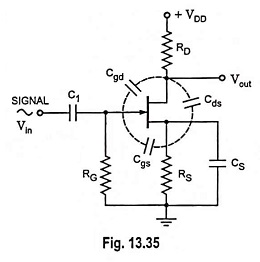
High Frequency Model: At low frequency, reactance offered by interelectrode capaci­tance is very large and, therefore, interelectrode capacitances do not appear in low frequency equivalent circuit. At higher fre­quencies device capacitances between terminals cause reduction in amplifier gain as capacitive impedance decreases with the in­crease in supply frequency. Such circuit capacitances resulted in due to device construction or stray wir­ing are shown as connected with dashed lines in the cir­cuit of Fig. 13.35 to indi­cate that they are not ca­pacitances that are con­nected into the circuit in­tentionally but arise as a result of the circuit and de­vice construction.

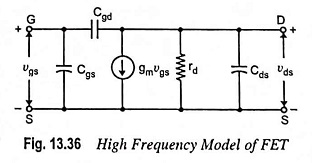
Figure 13.36 depicts the high frequency model of the FET which is identical with Fig. 13.32 except that the capacitances between the gate-source and gate-drain nodes are shown in the figure. The capacitor C_gs represents the barrier capacitance between gate and source, and C_gd is the barrier capacitance between gate and drain. The element C_ds represents the drain to source capacitance of the channel. Because of these internal capacitances feedback exists between the input and output circuits of the FET and voltage amplification drops drastically with increase in frequency.