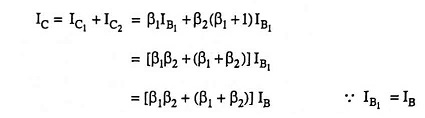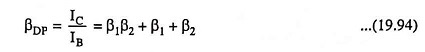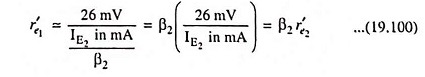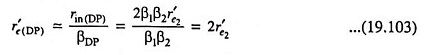Darlington Pair Transistor – Circuit Diagram and its Workings:

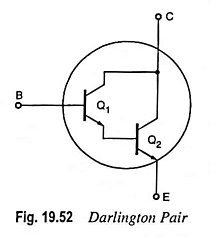
A very popular connection of two BJTs for operation as one “superbeta” transistor is the Darlington connection. In practice, the two transistors are put inside a single package and three terminals E, B and C are brought out, as de­picted in Fig. 19.52. The main fea­ture of the Darlington Pair Transistor connection is that the composite transistor acts as a single unit that has a high cur­rent gain (product of the current gains of the individual transistors) and high input impedance. The cur­rent gain provided by the Darlington connection is of the order of a few thousand.

Analysis:

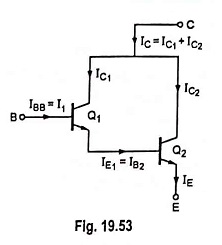
Let β₁ and β₂ be the dc values of transistors Q₁ and Q₂ respectively. Then by definition.

Collector current of transistor Q₁,

and Emitter current of transistor Q₁,

Base current of transistor Q₂,

So collector current of transis­tor Q₂,

Now collector current,

Effective β of Darlington Pair Transistor connection

From above Eq. (19.94) it is obvious that the effective β of the Darlington connection is product plus the sum of the βs of the individual transistors. It is usually true that β₁β₂ >> (β₁ + β₂) so

Darlington Pair Transistor are often fabricated on a single chip to achieve matched transistors Q₁ and Q₂ characteristics. For β₁ = β₂ = β, we have the effective β of the Darlington connection

It is assumed that the dc and small signal values of β are approximately equal.

Determination of Small-Signal Input Resistance From B to E, r_in(DP), and The Emitter Resistance r′_e(DP), of The Composite Transistor

We know that

AC resistance looking into the base of transistor Q₂,

Now

Since I_E2 = β₂I_B2 = β₂I_E1, we have

Substituting I_E1 = I_E2/β₂ in Eq. (19.99) we have

The total effective resistance looking into the base of transistor Q₁, (across the composite B-E terminals), i.e. the effective small-signal input resistance of the Darlington connection,

Substituting r′_e1 = β₂r′_e2 from Eq. (19.100) we have

Since β_DP ≈ β₁β₂, the effective emitter resistance