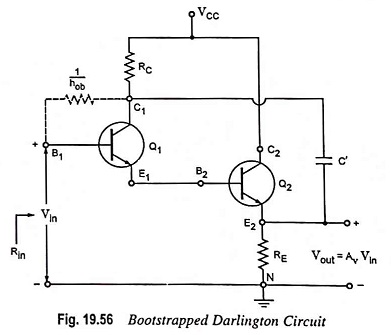
Bootstrapped Darlington Circuit Operation and its Equivalent Circuit:

The maximum input resistance of a Darlington circuit is limited to 1/h_ob ≡ 2 MΩ, as 1/h_ob is the resistance between base and collector. However, the input resistance can be largely increased by bootstrapped darlington circuit through the addition of capacitor C’ between the first collector terminal C₁ and the second emitter terminal E₂, as illustrated in Fig. 19.56.

The noteworthy point is that R_C is essential because in its absence R_E would be shorted to ground. If the input signal changes by V_in then E₂ changes by A_vV_in (assuming that reactance of C’ is negligible) and the collector changes by the same amount. Hence 1/h_ob is now effectively increased to 1/h_ob(1-A_v) ≡ 400 MΩ for a voltage gain of 0.995.

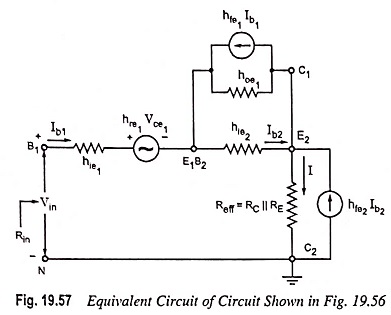
An expression for the input resistance R_in of the bootstrapped Darlington circuit can be had by using the equivalent circuit shown in Fig 19.57.

The effective resistance R_eff between terminal E₂ and ground is R_C || R_E. If h_oeR_eff ≤ 0.1, then transistor Q₂ may be represented by approximate hybrid model. However, the exact hybrid model, as shown in Fig. 19.57, must be used for Q₂. Since 1/h_oe1 >> h_ie2, h_oe1 may be omitted from this figure. Solving for V_in/I_b1, we have

The above equation shows that the input resistance of the bootstrapped Darlington circuit is essentially equal to the product of the short-circuit current gains and the effective emitter resistance. If the transistor with the current gains of the order of magnitude of 100 are used and effective resistance as 5 kΩ, then input resistance obtained would be of the order of 50 MΩ.