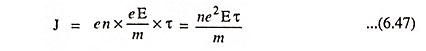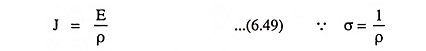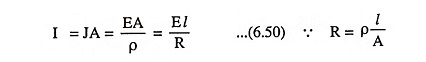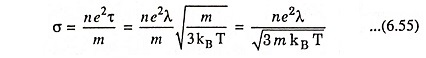Explain Conductivity of Metals:
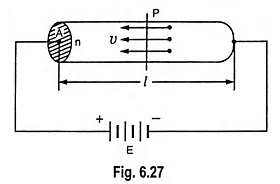
Conductivity of Metals – Consider a conductor of length l metres and cross-sectional area A square metres, as shown in Fig. 6.27. Let the number of free electrons available per m3 of the conductor material i.e., electron density be n and E be the applied electric field. Due to the applied electric field, let axial drift velocity of the electrons be v metres/second.
The force F on the particle of charge q when an electric field E is applied is given as F = qE, so the force acting on an electron having charge e on it is given as
Also
where a is acceleration of electrons due to applied field E
Combining Eqs. (6.39) and (6.40), we have
Acceleration,
Because of collisions of electrons during motion, the electrons will not get accelerated indefinitely. In fact, their velocity will fall to zero. If τ is the relaxation or collision time, the average velocity of electrons, known as drift velocity is given as
Let I be the current flowing through the conductor on application of electric field E corresponding to drift velocity v. In time dt, the electrons will travel a distance vdt and the number of electrons crossing the cross-sectional area A in time dt will be contained in volume Avdt. Thus, total charge flowing through the section in time dt
Since the current in a conductor is defined as the rate of change of charge per unit time, current I is given as
The current density J, defined as the current per unit area is given as
The above equation may also be written as
where ρ is the charge density in coulombs/m3 = en
Substituting the value of v from Eq. (6.42) in above Eq. (6.45), we have
For a particular material, the quantity ne2τ/m in above equation is constant at particular temperature and is known as electrical conductivity ‘σ’ of the material and thus
Current density,
So, the current density J is proportional to the Conductivity of Metals σ and the magnitude of applied electric field E. In terms of resistivity ρ, current density J is given as
We know that the resistance R of a conductor is given as R = ρ l/A where ρ is the resistivity of material and l is the length of conductor. Thus
Since E = V/l, the Eq. (6.50) may be written as
which is nothing but ‘Ohms’ law.
Electrical Conductivity of Metals is also given as
where μe = eτ/m is the mobility acquired by electrons due to presence of electric field.
Using Eq. (6.42), the mobility of electrons can also be expressed as
Thus, the mobility of electron in the metal is defined as the steady-state drift velocity per unit electric field.
Let λ be the mean free path and v’ be the root mean square velocity of electrons, then the relaxation time (commonly known as mean time between collisions) τ is given as
But
Now the electrical conductivity σ can be expressed as
Since electrical resistivity ρ is reciprocal of electrical Conductivity of Metals σ,
Above result shows that the resistivity varies as √T whereas actually it is found to vary linearly with temperature.