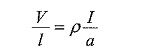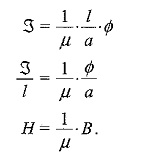Difference Between Electric Circuit and Magnetic Circuit:

A Difference Between Electric Circuit and Magnetic Circuit are shown in Figs. 10.27(a) and (b) respectively.

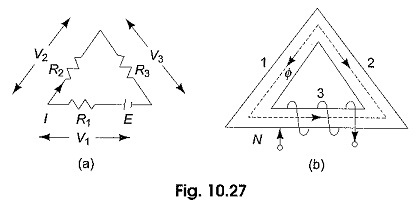
Figure 10.27(a) represents an electric circuit with three resistances connected in series, the dc source E drives the current I through all the three resistances whose voltage drops are V₁,V₂ and V₃. Hence, E = V₁ + V₂ + V₃, also E = I(R₁ + R₂ + R₃). We also know that R = ρl/a, where ρ is the specific resistance of the material, l is the length of the wire of the resistive material and a is the area of cross-section of the wire.

The drop across each resistor V = RI =ρl I/a

or

Voltage drop per unit length = specific resistance x current density.

Let us consider the magnetic circuit in Fig. 10.27(b). The MMF of the circuit is given by ζ = NI, drives the flux Φ around the three parts of the circuit which are in series. Each part has a reluctance R = 1/μ . l/a, where l is the length and a is the area of cross-section of each arm. The mmf of the magnetic circuit is given by ζ = ζ₁ + ζ₂ + ζ₃ . ζ = Φ(R₁ + R₂ + R₃) where R₁ R₂ and R₃ are the reluctances of the portion 1, 2 and 3 respectively.

Also

1/μ can be termed as reluctance of a cubic metre of magnetic material from
which, the above equation gives the mmf per unit length (intensity) which is analogous to the voltage per unit length. Parallels Difference Between Electric Circuit and Magnetic Circuit quantities are shown in Table 10.1.

Thus, it is seen that the magnetic reluctance is analogous to resistance, mmf is analogous to emf and flux is analogous to current. These analogies are useful in magnetic circuit calculations. Though we can draw many parallels between the two circuits, the following differences do exists.

The electric current is a true flow but there is no flow in a magnetic flux. For a given temperature, ρ is independent of the strength of the current, but μ is not independent of the flux.

In an electric circuit energy is expended so long as the current flows, but in a magnetic circuit energy is expended only in creating the flux, and not in maintaining it. Parallels between the quantities are shown in Table 10.1.