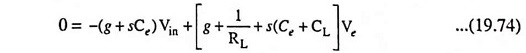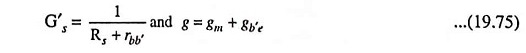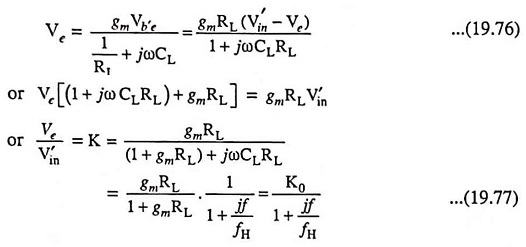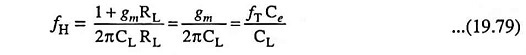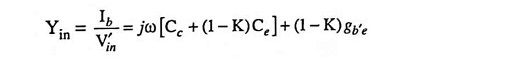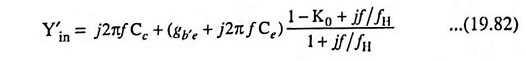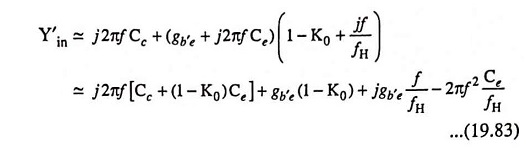Emitter Follower at High Frequencies:

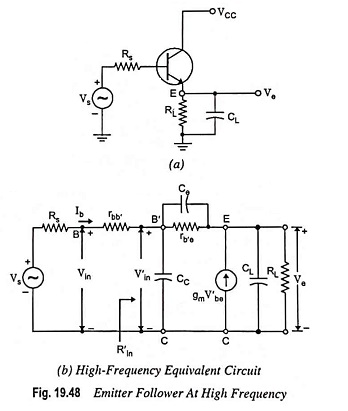
Emitter Follower at High Frequencies circuit is given in Fig. 19.48(a). A capacitance C_L is included across the load because the emitter follower is often used to drive capacitive loads. This is because of its small output impedance.

Applying Kirchhoff’s current law to nodes B′ and E respectively [Fig. 19.48(b)], we have

and

where

By elimination of V′_in from above equations, the voltage gain V_e/V_s is obtained in terms of s.

A very simple approximate expression for the transfer function can be obtained by applying Miller’s theorem to the circuit given in Fig. 19.48 (b).

The low frequency gain of an emitter follower is approximately equal to unity i.e. K ≈ 1 and K – 1 ≈ 0. Thus input time constant τ_in ≈ (R_s + r_bb′) C_c and the output time constant τ_out is proportional to C_L. Since load is assumed to be highly capacitive, τ_out >> τ_in. It means that the upper 3-dB frequency is determined to a good approximation, by the output circuit alone. Using K = 1, we have

where

and

Since we know, f_T = g_m/2πC_e, we see that τ_out = C_L/g_m and the condition τ_out >> τ_in needs

Since the input impedance between terminals B′ and C is very large in comparison to R_s + r_bb′, then K represents the overall voltage gain

A somewhat better approximation for f_H is given as

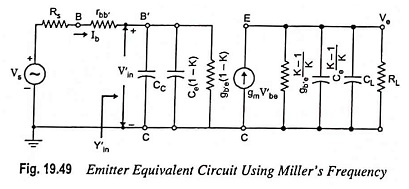
Input Admittance: Input admittance, excluding r_bb′, can be determined by making reference to Fig. 19.49.

Substituting the value of K from Eq. (19.77) in above equation, we have

Input admittance,

Since K₀ is approximately equal to unity, the numerator of Eq. (19.82) is affected by frequency at a much lower value of f than is the denominator. Thus, for f < f_H, Eq. (19.82) may be written as

where the last term represents a negative resistance which is a function of frequency. Thus, the input impedance consists of a capacitance shunted by a negative resistance. If the source resistance have some inductance in series with it, it is possible for the circuit to sustain undesirable oscillations. This condition can be avoided if we use a small resistance in series with R_s so that the net resistance seen by the source is positive.