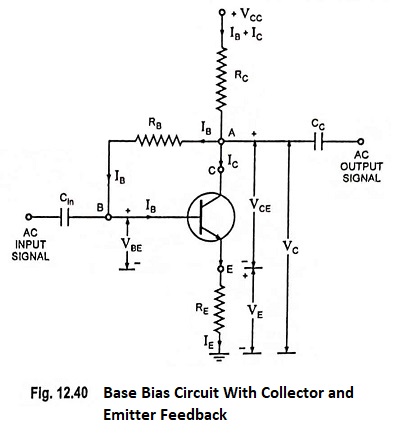
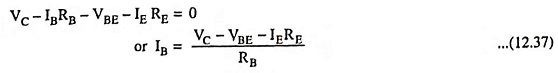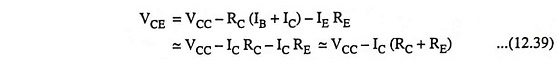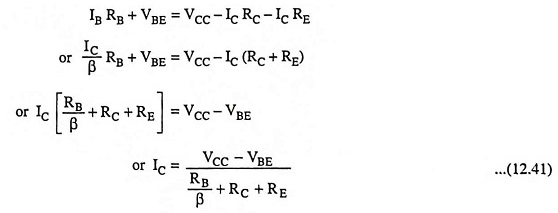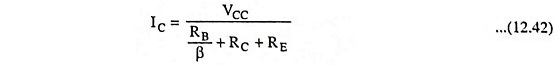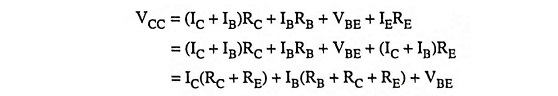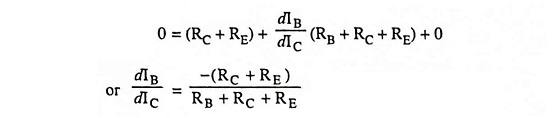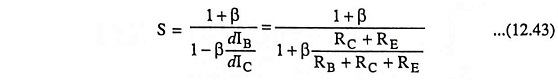Base Bias Circuit With Collector and Emitter Feedback:

In this Base Bias Circuit With Collector and Emitter Feedback circuit, as obvious from its name, both collector and emitter feedbacks are used in an attempt to reduce circuit sensitivity to changes in β. Increase in β causes increase in emitter voltage but decreases collector voltage. As a result voltage across base resistor R_B is reduced causing I_B to fall thereby partially compensating the increase in β.

In this Base Bias Circuit With Collector and Emitter Feedback circuit a current flows in resistance R_C from the supply V_CC. At point A this current divides itself in two parts, one flowing in the collector of transistor, l_C and the second part flows in the base resistor R_B, I_B. Thus current flowing in resistor R_C will be equal to I_B + I_C.

No current flows to the output terminals since coupling capacitor C_C offers infinite impedance to it (open circuit for dc).

Let the potential of point A be V_C.

Applying Kirchhoff’s second law from point A to ground via R_B, we have

Neglecting V_BE in comparison to collector potential V_C which is usually very small.

Now applying Kirchhoff’s second law for circuit starting from V_CC through collector to emitter terminal, we have

neglecting I_B being too small and I_E being almost equal to l_C.

Applying Kirchhoff’s second law to the circuit starting from collector point A to E via R_B

Comparing Eqs. (12.39) and (12.40) we have

Neglecting V_BE, being very small in comparison to supply voltage V_CC,

The quiescent point, Q is thus established.

The circuit also stabilizes itself. Let the temperature of transistor junction rise when it is loaded. The increase in temperature causes increase in I_C and β. When l_C increases voltage drop in collector resistance R_C i.e. l_C R_C increases and potential of collector drops. This causes reduction in value of base current I_B which in turn reduces I_C being equal to βI_B.

Stability factor S:

Applying KVL to the input side, we have

Differentiating above equation w.r.t. l_C we have

Substituting this value in general expression for S, we have