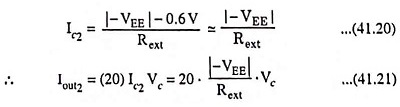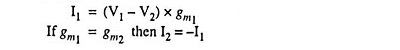OTA as Programmable Resistor, Grounded Resistor and Floating Resistor:

OTA as a Programmable Resistor: We may employ I_c OTA as a programmable resistor whose resistance is controlled by controlling current I_c.

We can define resistance, using Eq. (41.16)

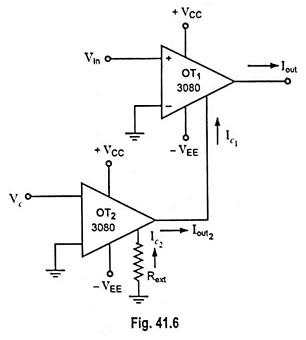
Two OTAs can be employed to behave as programmable resistor, as shown in Fig. 41.6.

Now to derive expression for resistance consider first the OTA IC OT₂.

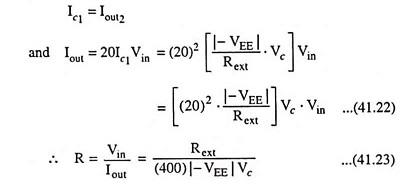
For the other IC 3080 OT₁ say,

Here V_in must be less than 20 mV and I₀ < 400 μA.

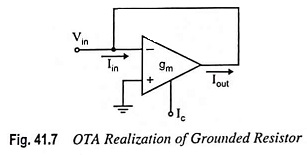
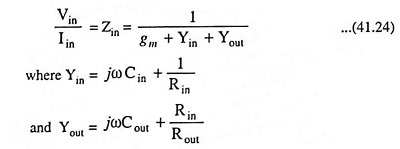
OTA Circuit for Realization of a Grounded Resistor: Figure 41.7 shows an OTA circuit that realizes a grounded resistor with a value that can be controlled by current I_c.

The input impedance is

For frequencies low enough and parasitic resistances large enough, Z_IN ≈ 1/g_m.

If the input leads of the OTA are interchanged, the circuit yields a short circuit stable negative resistor with Z_IN ≈ 1/g_m.

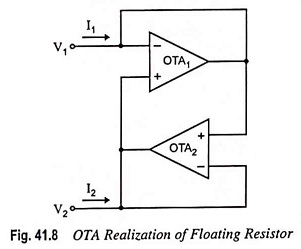
OTA Circuit for Realization for a Floating Resistor: Figure 41.8 depicts a circuit that can realize a floating resistor.

Using the ideal model and solving for I₁ and I₂, we have

and the circuit realizes a floating resistor of value 1/g_m.

The two circuits shown in Figs. 41.7 and 41.8 permits the construction of active filters without the use of resistors. Thus, transconductance C filters can be realized and such filters are attractive for monolithic I_c realizations.

For active filters, adders (summers) and integrators are also required which are discussed in the forthcoming sections.