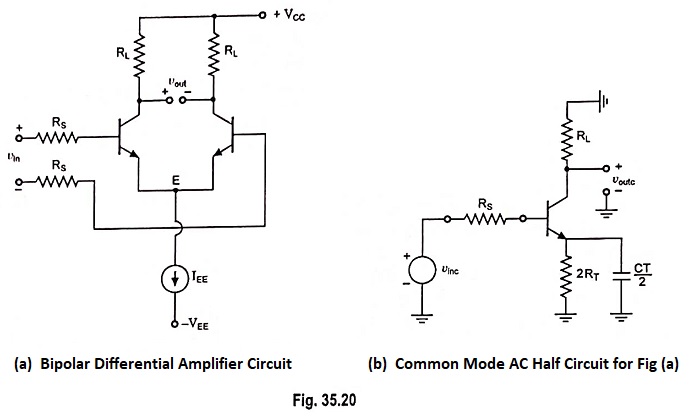
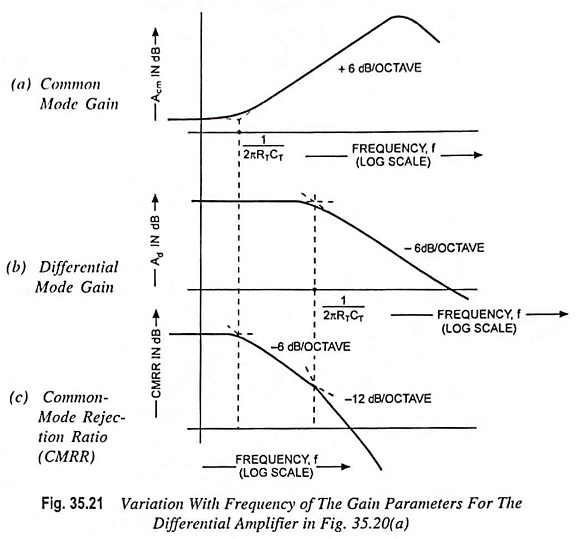
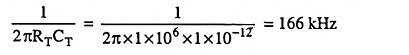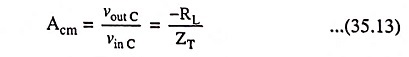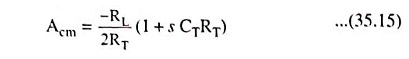Frequency Response of Common Mode Gain of Differential Amplifier:

Low values of common-mode gain are desirable so that the circuit can reject undesirable signals that are applied equally to both inputs. The common-mode (CM) gain becomes important because undesired common-mode signals may have high-frequency components.

The important aspects of the Frequency Response of Common Mode Gain of Differential Amplifier can be calculated with some approximations. Consider the time constant=R_TC_T, where R_T and C_T are the equivalent output resistance and capacitance of the tail current source and R_T is usually greater than or equal to output resistance of a transistor.

Let us assume that the resistance R_T is of the order 1 MΩ. The capacitor C_T includes capacitance of current source transistor typically C_T = 1 pF or less.

Thus time constant = R_TC_T = 1 MΩ x 1 pF = 1 μs and the break frequency corresponding to this time constant is

Below this frequency the impedance Z_T is dominated by R_T, and above this frequency C_T dominates. Thus as the operating frequency is increased, the impedance Z_T will exhibit frequency variation before the rest of the circuit.

Assume that C_T is the only significant capacitance. Since the impedance Z_T is high, almost all of v_{in c} appears across Z_T if source resistance R_s is small. Thus common-mode gain can be approximated as

where

From Eqs. (35.13) and (35.14) we have

Above Eq. (35.15) reveals that the common-mode gain expression contains a zero, which causes the common-mode gain to rise at 6 dB/octave above a frequency ω = 1/R_TC_T. This behavior is undesirable because the common-mode gain should ideally be as small as possible.

The CMRR is plotted as a function of frequency in Fig. 35.21(c) by simply taking the magnitude of the ratio of the differential mode (DM) and CM gains. This quantity begins to decrease at frequency f = 1/2πR_TC_T when |A_cm| begins to increase. The rate of decrease of CMRR further increases when |A_d| begins to fall with increasing frequency. Thus differential amplifiers are far less able to reject CM signals as the frequency of those signals increases.