Foster Seeley Detector – Circuit Diagram, Working and its Phasor Diagram:

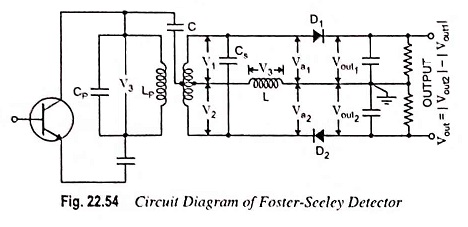
The circuit diagram of the Foster Seeley detector is shown in Fig. 22.54. This Foster Seeley Detector circuit consists of an inductively coupled double tuned circuit in which both primary and secondary coils are tuned to the same frequency (intermediate frequency).

The centre of the secondary coil is connected to the top of the primary (collector end) through a capacitor C. This capacitor C performs the following functions:

1. It blocks the dc from primary to secondary.
2. It couples the signal frequency from primary to centre tapping of secondary.

The primary voltage V₃ (i.e., the signal voltage) thus appears across the inductor L. Nearly entire voltage V₃ appears across inductor L except a small drop across the capacitor C. However, by a suitable choice of C and L, the voltage drop across the capacitor C can be made negligible.

The centre tapping of the secondary coil has an equal and opposite voltage across each half winding. Hence V₁ and V₂ are equal in magnitude but opposite in phase. The radio frequency voltages V_a1 and V_a2 applied to the diodes D₁ and D₂ are expressed as

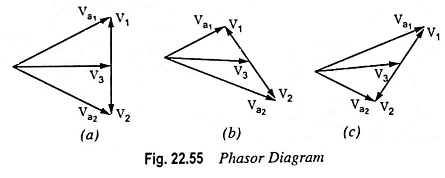
Voltage V_a1 and V_a2 depend upon the phase relations between V₁, V₂ and V₃. The phasor diagrams of Foster Seeley Detector for different frequencies have been shown in Fig. 22.55. The phasors V₁ and V₂ are always equal in magnitude but in phase opposition. However, the phase position of V₁ and V₂ relative to V₃ would depend upon the tuned secondary coil at the resonance or off the resonance as discussed below :

1. At Resonance: When an input voltage has a frequency equal to the resonant frequency f_if of the tuned secondary, V₃ is in phase quadrature (90° out of phase) with V₁ and V₂. This has been indicated in Fig. 22.55 (a). The resultant voltages V_a1 and V_a2 are equal in magnitude.

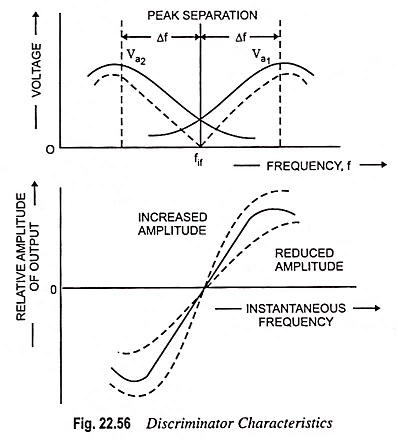
2. Off Resonance: When the input voltage is off the resonant frequency f_if of the tuned secondary, the phase position of V₁ and V₂ relative to V₃ will be different from 90°. Let Q_s be the quality factor of tuned secondary coil. When an input signal frequency exceeds the resonant frequency f_if by an amount f_if/2Q_s the phase difference between V₃ and V₁ is 45° as shown in Fig. 22.55 (b). Because V₂ is in phase opposition of V₁, the phase difference between V₃ and V₂ is 135°. The phasor diagram shown in Fig. 22.55 (b) reveals that V_a1 is reduced whereas V_a2 is increased. The situation is reversed when the input voltage has a frequency below f_if which is evident from the phasor diagram shown in Fig. 22.55 (c). Thus the magnitude of the voltages V_a1 and V_a2 will vary with the instantaneous frequency f in the manner shown in Fig. 22.56.

The RF voltages V_a1 and V_a2 are separately rectified by the diodes D₁ and D₂ respectⁱvely to provide voltages V_out1 and V_out2. The RF components are bypassed by the capacitors leaving only modulating frequency component and a dc term. The voltages V_out1 and V_out2 then represent the amplitude variations of voltages V_a1 and V_a2 respectively. The diodes are so arranged that the output voltage V_out is equal to the arithmetic difference | V_out2 | – | V_out1 |.

Thus, the output voltage V_out will vary with instantaneous frequency in accordance with the difference | V_out2 | – | V_out1 |, as shown by the dotted curve in Fig. 22.56 (b). This allotted curve is known as discriminator characteristic in Fig. 22.56.