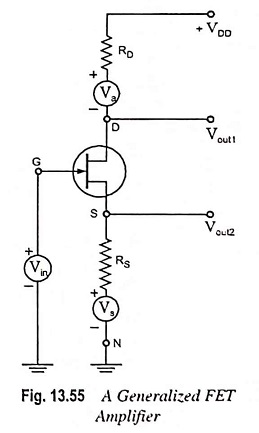
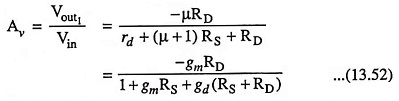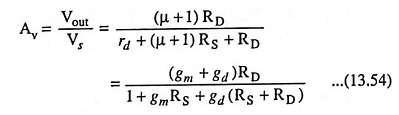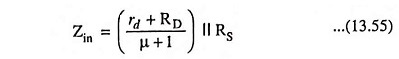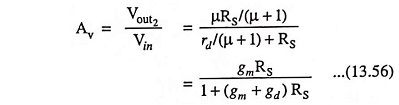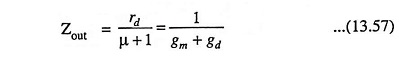Generalized FET Amplifier Circuit:

The analysis of a common source amplifier with a source resistance R_S, a common gate amplifier and a common drain amplifier at low frequencies may be made by considering the Generalized FET Amplifier Circuit given in Fig. 13.55. The Generalized FET Amplifier Circuit consists of three independent signal sources (V_in in series with the gate, V_s in series with the source, and V_a in series with the drain).

For common source amplifier V_a = V_s = 0, and the output V_out1 is taken at the drain terminal D, as shown. For common gate circuit V_in = V_a = 0, the input signal is V_s with a source resistance R_S, and the output V_out1 is again taken at the drain terminal D. For the common drain (or source follower) R_D = 0, V_s = V_a = 0, the input signal voltage is V_in and the output V_out2 is taken at the source terminal, as shown in Fig. 13.55. The signal-source resistance is ineffective as it is in series with the gate which draws almost no current.

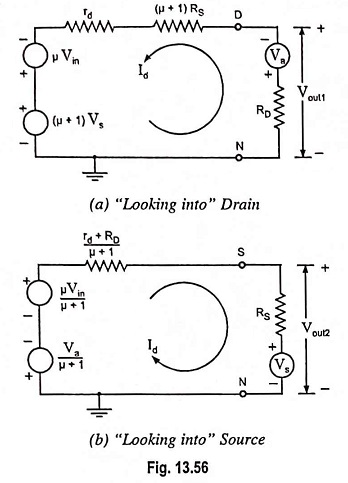
Thevenin’s equivalent circuit from drain to ground and from source to ground are given in Figs. 13.56 (a) and 13.56 (b) respectively. From the circuit given in Fig. 13.56 (a) it is concluded that “looking into the drain” of the FET it is seen (for small signal operation) an equivalent circuit consisting of two generators in series, one of -μ times the gate signal voltage V_in and the second (μ + 1) times the source-signal voltage V_s and the resistance r_d+(μ + 1) R_S. Note that the source-signal voltage V_s and the resistance in the source lead are both multiplied by the same factor, (μ + 1).

1. Common Source Amplifier With An Unbypassed Source Resistor:

In Fig. 13.56 (a) substituting V_a = V_s = 0, we have

Voltage gain

Note that, for R_S = 0, the above equation reduces to that Eq. (13.41). The minus sign indicates a phase shift of 180° between input and output.

Resistance R_out, looking into the drain is increased by (μ + 1)R_S from its value r_d for R_S = 0. The net output resistance R′_out taking R_D into account is given as

It is observed that with the addition of R_S, voltage gain is reduced while the output impedance is increased. The input impedance is extremely high (100 MΩ or so) since gate junction is reverse biased.

2. Common Gate Amplifier:

In Fig. 13.56 (a) substituting V_in = V_a = 0, we have

Voltage gain,

Since A_v is positive, there is no shift between input and output. Also since g_m ≫ g_d, the magnitude of amplification is approximately the same as for the common source amplifier circuit with R_S ≠ 0.

The output resistance is given by Eq. (13.53), and unless R_S is quite small, output resistance will be much larger than r_d || R_D.

The input impedance Z_in, between source and ground is obtained from seeing Fig. 13.56 (b)

The common gate amplifier with its low input impedance and high output impedance has few applications.

Output From Source: From Fig. 13.56 (b) it is concluded that “looking into the source” of the FET it is seen (for small-signal operation) an equivalent circuit consisting of two generators in series, one of value µ/(µ + 1) times the gate-signal voltage v_in and the second 1/μ + 1 times the drain-signal voltage v_a and a resistance r_d + R_D/μ + 1.

3. Common Drain Amplifier:

Substituting V_s = V_a = 0 and R_D = 0 in Fig. 13.56 (b), we have

Voltage gain,

The output impedance Z_out of the source follower at low frequencies (with R_D = 0 and with R_S considered external to the amplifier) is, from Fig. 13.56 (b),