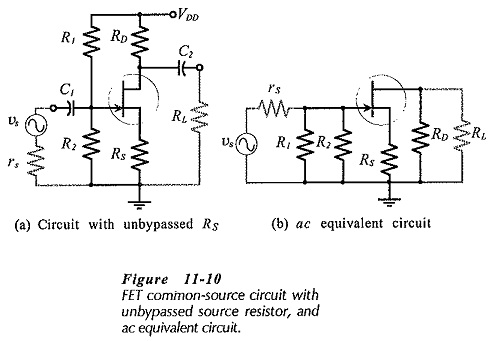
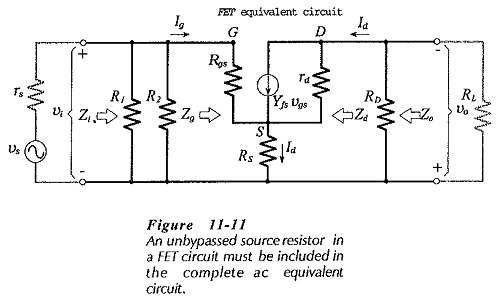
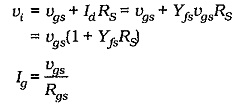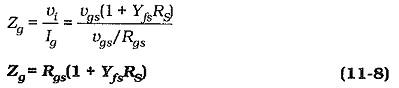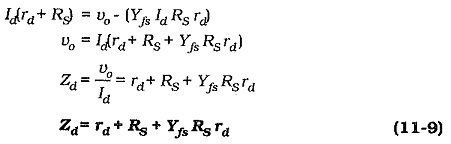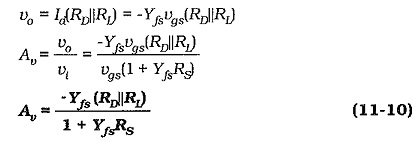FET Common Source Amplifier with Unbypassed Source Resistors:

Equivalent Circuit – When an unbypassed source resistor (R_S) is present in a FET Common Source Amplifier circuit, as shown in Fig.11-10(a), it also appears in the ac equivalent circuit, [Fig. 11-10(b)].

In the complete equivalent circuit R_S must be shown connected between the FET source terminal and the circuit common input-output terminal, (Fig. 11-11). As with the previous equivalent circuit, the current directions and voltage polarities shown in Fig. 11-11 are those that occur when the instantaneous input voltage is positive-going. The presence of R_S without a bypass capacitor significantly affects the circuit voltage gain.

Input Impedance:

An equation for the input impedance at the FET gate can be determined from v_i and I_g. From Fig. 11-11,

Equation 11-8 gives the input impedance at the FET gate terminal. The circuit input impedance is again given by,

In this case, Z_g is much larger than R₁||R₂, so the circuit input impedance is determined by the gate bias resistors.

Output Impedance:

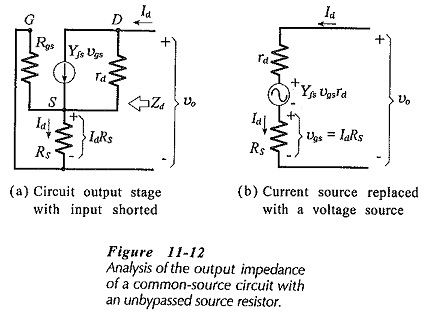
To calculate the circuit output impedance, the ac signal voltage (v_s) is assumed to be zero, and an ac voltage (v_o) is applied at the output, (see Fig. 11-12(a)]. The ac output current (I_d) is calculated in terms of v_o, then Z_o is determined as v_o divided by I_d. Figure 11-­12(a) shows that when v_s is zero, the ac voltage across source resistor R_S is applied as a gate-source voltage

Actually, I_dR_S is divided across r_s||R_G and R_gs. However, R_gs ≫r_s || R_G, so that all of I_dR_S is effectively applied as a gate-source voltage. The v_gs produced in this way generates an ac drain current which opposes the drain current produced by v_o,

Converting the current generator [(Y_fsv_gs) in parallel with r_d] to a voltage generator [(Y_fsv_gsr_d) in series with r_d] gives the equivalent circuit in Fig. 11-12(b). The equation for the voltage drops around this circuit is,

The circuit output Impedance is,

Because the output impedance at the FET drain terminal is much larger than the drain resistor (R_D), the output impedance of the circuit with the unbypassed source resistor is still,

Voltage Gain:

From the derivation of the input impedance equation,

and neglecting r_d,

Usually,

The voltage gain of a FET Common Source Amplifier circuit with an unbypassed source resistor can be quickly estimated using Eq. 11­-11. For the circuit in Fig. 11-10(a), with R_D = 4.7 kΩ, R_S = 2.2 kΩ, and R_L ≫ R_D, A_v ≈ -2.1.

Summary of Performance of CS Circuit with Unbypassed R_S

The most significant feature of the performance of a CS circuit with an unbypassed source resistor is that its voltage gain is much lower than that for a CS circuit with R_S bypassed.