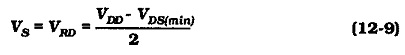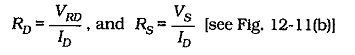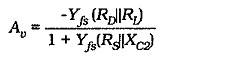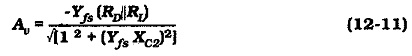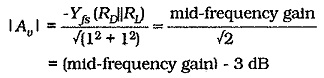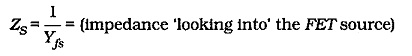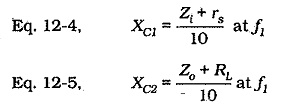Single Stage Common Source Amplifier:
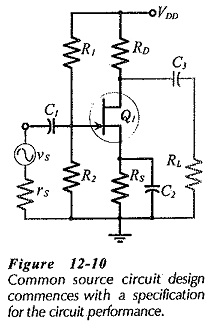
Bias circuit design for the Single Stage Common Source Amplifier in shown in Fig. 12-10. As with the common-emitter BJT circuit, design commences with specification of the supply voltage, amplification, frequency response, load impedance, etc.
Selection of ID,RD, and Rs
The circuit shown in Fig. 12-10 has no provision for negative feedback, so, it should be designed to achieve the largest possible gain. The voltage gain of a CS circuit is,
Because Av is directly proportional to RD||RL, design for the greatest voltage gain normally requires selection of the largest possible drain resistance. However, a very large value of RD might make the drain current too small for satisfactory FET operation. Also, low ID levels give small Yfs values, which result in lower ac voltage gain. Furthermore, RD should normally be much smaller than RL, so that RL has little effect on the circuit voltage gain.
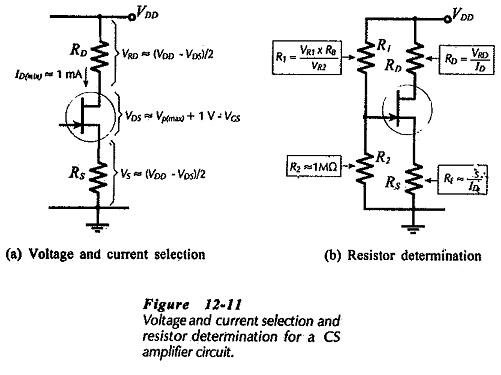
For a given level of ID, the largest possible voltage drop across RD gives the greatest RD value, (RD = VRD/ID). To make VRD as large as possible, VDS and VS should be held to a minimum, (see Fig. 12-11(a)]. The drain-source voltage should typically be VDS(min) = (VP(max) + 1 V). This is large enough to ensure that the FET operates in the pinch-off region of its characteristics. It also allows for a drain voltage swing of ±1 V, which is usually adequate for a small-signal amplifier. If the gate-source bias voltage (VGS) is other than zero, then, as illustrated in Fig. 12-11(a), the minimum VDS should be calculated as,
Recall from earlier article that for good bias stability, the source resistor voltage drop (VS) should be as large as possible. Where the supply voltage is small, VS may be reduced to a minimum to allow for the minimum level of VDS. A reasonable approach for most FET circuits is to calculate the the sum of VS and VRD from,
and then make,
Once VS, VRD, and ID are selected, RD and RS are calculated,
As already discussed, a bias line should be drawn upon the FET transfer characteristics to determine a suitable gate bias voltage (VG). The selected maximum drain current (ID(max)) is plotted on the maximum transfer characteristics for the FET used. The bias line is then drawn through this point with a slope of 1/Rs. The gate bias voltage is read from the intersection of the bias line and the VG scale. As an alternative to drawing the bias line, VGS can be read from the transfer characteristic when ID(max) is plotted. Then,![]()
Instead of using the FET transfer characteristics, VP(max) and IDSS(max) can be substituted to calculate the VGS level.
Bias Resistors:
With a voltage divider bias circuit [as in Fig. 12-11(13)], R2 is usually selected as 1 MΩ or less. Smaller resistance values may be used where a lower input impedance is acceptable. Larger resistance values may also be used, however, as discussed earlier, there are distinct disadvantages to using resistances higher than 1 MΩ. With R2 determined, R1 is calculated using R2 and the ratio of VR1 to VR2.
Capacitors:
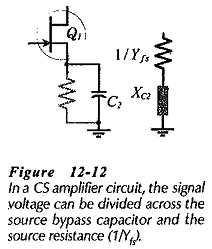
As for a BJT capacitor-coupled circuit, coupling and bypass capacitors should be selected to have the smallest possible capacitance values. The largest capacitor in the circuit (source bypass capacitor C2 in Fig 12-10) sets the circuit low 3 dB frequency (f1). Equation 11-10 was developed for the voltage gain of a Single Stage Common Source Amplifier with an unbypassed source resistor (RS). Rewriting the equation to include XC2 in parallel with RS gives
Normally RS ≫ XC2, so RS can be omitted. Also, XC2 is capacitive,
When YfsXC2 =1,
Therefore, at f1,
From Section 11-7,
So, at f1,
Equations 12-12 gives the smallest value for the source bypass capacitor. When selecting a standard value, the next larger capacitance value should be chosen. This will give a cutoff frequency slightly lower than the f1 value used in the calculations.
As explained in earlier, it is important to note that the bypass capacitor is calculated in terms of the resistance seen looking into the device terminal (the resistance in series with C2). The capacitance value is not determined in terms of the parallel resistor (RS).
The input and output coupling capacitors should have almost zero effect on the circuit frequency response. It is explained that XC1 in series with Z1 and XC3 in series with RL, constitute voltage dividers that can attenuate the ac input and output voltages. To minimize the attenuation, the reactance of each coupling capacitor is selected to be approximately one-tenth of the impedance in series with it at the lowest operating frequency for the circuit (f1). Equations 12-4 and 12-5 apply once again for the calculation of the minimum C1 and C2 values.
As in BJT circuits, RL is usually much larger than Zo, and Zi is often much larger than rs, so Zo and rs can be omitted in Equations 12-4 and 12-5. As always, the equations give minimum capacitance values, so that the next larger standard values should always be selected for C1 and C3.