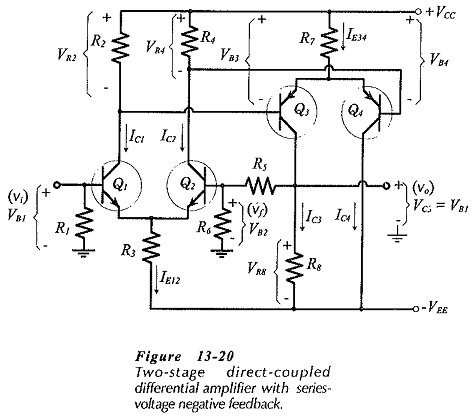
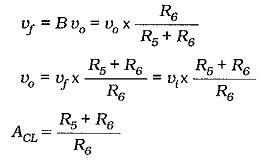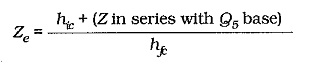Two Stage Differential Amplifier with Negative Feedback:

The circuit shown in Fig. 13-20 has a Two Stage Differential Amplifier with Negative Feedback with npn BJTs, and a direct-coupled pnp transistor differential amplifier second stage. The circuit uses a plus/minus supply voltage, and the base terminals of Q₁ and Q₂ are biased to ground via resistors R₁ and R₆, respectively. Transistors Q₃ and Q₄ have the bases directly connected to the collector terminals of Q₁ and Q₂. So, bias voltage for Q₃ and Q₄ bases is provided by the voltage drops across the Q₁ and Q₂ collector resistors, (R₂ and R₄).

The amplifier input terminal is the base of Q₁, and the output is taken from Q₃ collector. No collector resistor is provided for Q₄, because no output or feedback is taken from Q₄. Note that the feedback network (R₅ and R₆) is connected from the output at the collector of Q₃ back to the base of Q₂. Because the emitter of Q₂ is directly coupled to Q₁ emitter, applying the feedback voltage (v_f) to Q₂ base is similar to applying it to Q₁ emitter.

DC Bias Conditions:

The circuit in Fig. 13-20 is designed to have the do bias voltage at Q₂ base equal to Q₁ base bias voltage; in this case, ground level. This means that the do voltage at the collector of Q₃ must also equal the Q₁ base voltage, because Q₃ collector is directly connected to Q₂ base via R₅. Consider what would happen if V_C3 (at the output terminal ) is not exactly equal to V_B1 (at the input).

Suppose V_C3 goes lower than its normal level:

• V_B2 is reduced below the level of V_B1, and this reduces I_C2 and increases I_C1.
• The increased level of I_C1 causes an increased voltage drop across R₂, and the reduced level of I_C2 decreases the voltage drop across R₄. Thus V_B3 is increased and V_B4 is decreased.
• This raises the level of I_C3 and lowers I_C4. So, V_RB is increased (by the I_C3 increase) to drive V_C3 back up to its normal voltage. Similarly, if V_C3 somehow drifts to a higher than normal level:
• V_B2 is raised above the level of V_B1, thus increasing I_C2 and reducing I_C1.
• The decreased level of I_C1 and increased level of I_C2 produces voltage drops across R₂ and R₄ that reduce V_B3 and increase V_B4.
• This change reduces I_C3, thus decreasing V_RB to drive V_C3 back down to its normal voltage.

It is seen that there is do negative feedback that stabilizes the circuit bias conditions.

AC Operation:

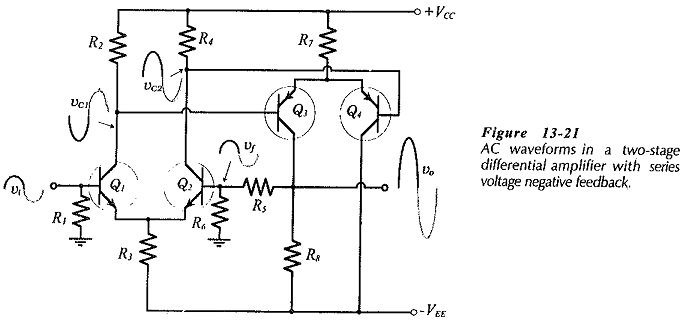
Consider the circuit waveforms shown in Fig. 13-21. A positive-going input signal (v_i) at the base of Q₁ produces a positive-going output (v_o) at Q₃ collector. As in the case of the dc bias conditions, the instantaneous ac voltage at Q₂ base follows the instantaneous level of the ac signal voltage at Q₁ base.

With v_b2 = v_b1, or v_i = v_f,

Resistors R₅ and R₆ in Figs. 13-20 and 13-21 are comparable to R_F1 and R_F2, respectively, in the other negative feedback circuits already discussed. So, the closed-loop gain equation is the same equation that applies in the case of all series-voltage negative feedback amplifiers. As always, the equation is true only when the open-loop gain is very much larger than the closed-loop gain.

The input and output impedances for a circuit with a Two Stage Differential Amplifier with Negative Feedback are calculated exactly as discussed for other negative feedback circuits.

Note that there are no bypass capacitors in the circuit in Figs. 13-20 and 13-21. If the signal and load are capacitor coupled to the circuit, the coupling capacitors determine the lower cutoff frequency. If the signal and load are direct coupled, then the circuit is a dc amplifier; one that amplifies direct voltage signals.

Circuit Design:

The second stage components are determined in essentially the same way as the input stage components, bearing in mind that the second stage is upside down compared to the input stage. Feedback network resistor R₆ at the base of Q₂ is selected equal to bias resistor R₁ at Q₁ base. This is to equalize the resistances at the bases of Q₁ and Q₂, and thus equalize any voltage drops due to I_B1 and I_B2. R₅ is calculated from the specified closed loop gain and the R₆ resistance.

Modification for Reduced Z_out:

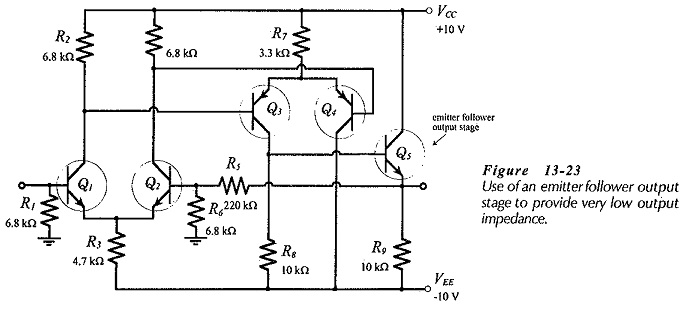
Although the application of series-voltage negative feedback substantially reduces the output impedance of a circuit, further reduction of Z_out is sometimes required. Figure 13-23 shows the circuit of Fig. 13-22 with the addition of an emitter follower output stage (Q₅). Note that the feedback network is now connected at the emitter follower output terminal.

The output impedance at Q₅ emitter terminal in Fig. 13-23 is found from the common-collector circuit

This gives,

This quantity is modified by negative feedback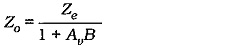

Then, as always, the circuit output impedance which must also be rewritten for the circuit in Fig. 13-23.

An emitter follower output stage can be added to any of the amplifiers previously discussed. However, the combination of an emitter follower output stage with a differential amplifier has a particular significance.