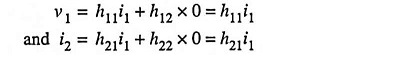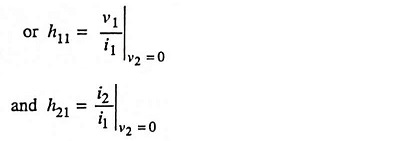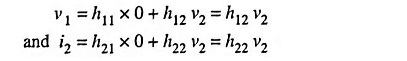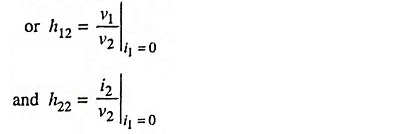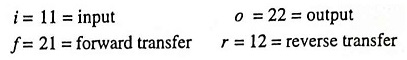Hybrid Parameters of Transistor or h Parameters and Hybrid Model:

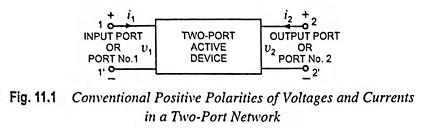
A box representing a two-port network is illustrated in Fig. 11.1. The terminal behavior of a two-port device may be specified by two voltages and two currents (voltage v₁, and current i_i at the input port and voltage v₂ and current i₂ at the output port). The conventional positive polarities of voltages v₁ and v₂ and currents i₁ and i₂ are shown in the figure. Out of four quantities (v₁, v₂, i₁ and i₂), any two may be selected as independent variables and the remaining two be expressed in terms of the selected independent variables. This leads to various two-port parameters, out of which following three are more important.

1. Open-circuit impedance parameters or Z-parameters Z₁₁, Z₁₂, Z₂₁ and Z₂₂
2. Short-circuit admittance parameters or Y-parameters Y₁₁, Y₁₂, Y₂₁ and Y₂₂
3. Hybrid parameters or the h parameters.

In transistor amplifier analysis, Z- and Y-parameters were used earlier. But now Hybrid Parameters of Transistor or the h parameters alone are used in a transistor circuit analysis and, therefore, only the h parameters will be taken here for discussion.

Hybrid Parameters of Transistor or h Parameters:

For the two-port network illustrated in Fig. 11.1, if input current i₁ and the output voltage v₂ are taken as independent variables and the two-port shown in the figure is linear, we may write

In the above equations, the hs are fixed for a given circuit and are called the Hybrid Parameters of Transistor or h parameters. Because these four parameters have mixed dimensions (h₁₁ has dimension of ohm, h₁₂ and h₂₁ are dimensionless, and h₂₂ has dimension of mho or siemen) so they are called Hybrid Parameters of Transistor or h parameters.

1. Meaning of h Parameters: By assuming that the given two-port network has no reactive element and by applying open circuit (i₁ = 0) or short circuit (v₂ = 0) conditions to Eqs. (11.1) and (11.2), the h parameters can be defined as below :

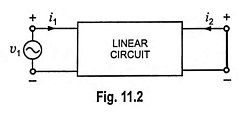
If the output terminals are short circuited, (Fig. 11.2) output voltage v₂ becomes zero and Eqs. (11.1) and (11.2) become

Since h₁₁ is the ratio of input voltage and input current with output terminals short circuited, it is called the input impedance with output short circuited. The subscript 11 of h₁₁ defines the fact that the parameter is determined by the ratio of quantities measured at the input terminals. Its unit is ohm.

Similarly h₂₁ is the ratio of output and input currents (i.e. i₂/i₁) with output terminals short circuited, so it is called the forward transfer current gain with output short circuited. Obviously it is dimensionless quantity.

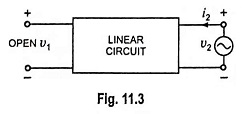
If the input terminals are open circuited and we drive the output terminals with voltage v₂, as shown in Fig. 11.3, input current i₁ becomes zero and Eqs. (11.1) and (11.2) become

Thus the parameter h₁₂ is the ratio of input voltage to the output voltage with zero input current (i.e. i₁ = 0). It is dimensionless quantity and is called the open-circuit reverse transfer voltage ratio, the subscript 12 of h₁₂ reveals that the parameter is a transfer quantity determined by the ratio of input to output measurements.

Similarly h₂₂ is the ratio of output current to the output voltage with zero input current (i.e. i₁ = 0). It is called the open-circuit output admittance and is measured in siemens. The subscript 22 in h₂₂ indicates that it is determined by a ratio of output quantities.

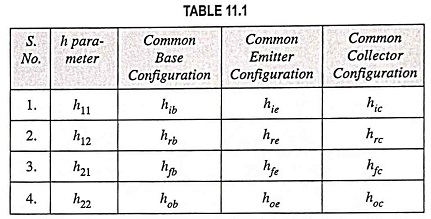
2. Notations: The convenient alternative subscript notations recommended by the IEEE Standards are given below:

In case of transistors, another subscript (b, e or c) is added to designate the type of transistor configuration. For example h_ie = h_11e = input resistance in common-emitter configuration.

Notations used in transistor amplifier for the three configurations are tabulated in Table 11.1.

Since the two-port network (or the device) described by Eqs. (11.1) and (11.2) is assumed to have no reactive elements, the four parameters h₁₁, h₁₂, h₂₁ and h₂₂ are real numbers and voltages and currents v₁, v₂, and i₁, i₂ are functions of time. However, if the reactive elements had been included in the device, the excitation would be considered to be sinusoidal, the h parameters would in general be functions of frequency, and the voltages and currents would be represented by phasors V₁, V₂, and I₁, I₂.

Hybrid Model:

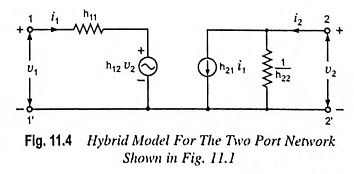
The hybrid circuit for any two-port network characterized by Eqs.(11.1) and (11.2) is shown in Fig. 11.4. If Kirchhoff s voltage law and Kirchhoff’s current law are applied to the input and output ports, Eqs. (11.1) and (11.2) respectively will be obtained. Thus model given in Fig. 11.4 truely satisfies Eqs. (11.1) and (11.2).

The input circuit derived from Eq. (11.1) appears as a resistance h₁₁ in series with a voltage generator h₁₂v₂. The output circuit, derived from Eq. (11.2) consists of a current generator h₂₁i₁ and shunt resistance 1/h₂₂. This circuit is called hybrid equivalent because its input portion is a Thevenin’s equivalent (or a voltage generator in series with a resistance) while the output portion is a Norton’s equivalent (or a current generator with shunt resistance). Thus it is a mixture or hybrid. The symbol ‘h’ is simply the abbreviation of the word hybrid (hybrid means “mixed”).

The hybrid equivalent circuit (or model) given in Fig. 11.4 is an extremely important one in the area of electronics today. It will appear over and over again in the analysis to follow. There are two main reasons of popularity of hybrid model. First, it isolates the input and output circuits, their interaction being accounted for by the two controlled voltage and current sources—the effect of output upon input is represented by the equivalent voltage generator h₁₂v₂ and the effect of input upon output is represented by the current generator h₂₁i₁. The value of the former depends upon the output voltage v₂ while the value for the latter depends upon the input current i₁. Secondly, the two portions of the circuit are in a form which makes it simple to take into account the source and the load circuits.