Two Port Network Parameters:

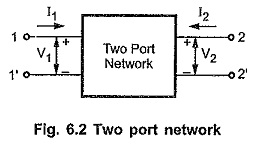
Consider a Two Port Network Parameters as shown in the Fig. 6.2. In all there are four variables; two voltages and two currents. In general, any two port network has one pair of voltage and current at each port.

To start with the discussion, we will first assume that other voltages and currents inside the box are not available for the measurements. Secondly it is assumed that the network consists only the linear elements along with dependent sources but independent sources are not allowed.

Also it is assumed that the initial conditions on capacitor and inductor present in the network are zero.

Assuming the variables at input and output ports as transformed quantities, the voltage and current at input terminals are V₁ and I₁ while at output terminals are V₂ and I₂, as shown in the Fig. 6.2. The directions of both the currents I₁ and I₂ are assumed to be flowing into the network.

In order to describe the relationship between port voltages and currents one requires the linear equations equal to the number of ports. So in two port network analysis, we will require two linear equations interms of four above mentioned variables.

We can obtain these equations by considering two variables as dependent variables while other as independent variables. As the network consists only linear elements, the linear relationship can be obtained by writing two variables in terms of other two variables.

There are six possible ways of selecting two independent variables out of four variables. Thus there are six different pairs of equations defining their own sets of parameters such as impedance (Z), admittance (Y), hybrid (h), inverse hybrid (g), transmission and inverse transmission parameters.