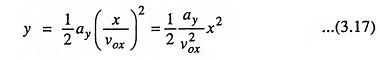Two Dimensional Motion in a Uniform Electric Field:

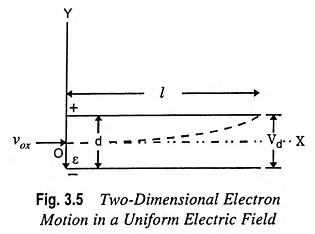
Two Dimensional Motion in a Uniform Electric Field – Let us consider that an electron enters the region between two parallel plates of a parallel plate capacitor oriented as illustrated in Fig. 3.5 with an initial velocity v_ox m/s in the +X direction. It is assumed that the electric field ε between the plates is uniform and, as chosen, it is in the direction of –Y axis, no other fields existing in the region.

The initial condi­tions, at t = 0, are as­sumed to be

Since there is no force in the Z direc­tion, the acceleration in that direction is zero and, therefore, the component of veloc­ity in the Z direction remains constant. Since the initial velocity in this direction is assumed to be zero, the motion must take place entirely in one plane, the plane of the paper or X-Y plane.

For a similar reason the velocity along the X-axis remains constant and is equal to v_ox i.e.,

It means that the distance moved in time t in X-direction is

On the other hand, a constant acceleration exists along the Y-direction, and the two dimensional motion in a Uniform Electric Field is given by equation

and

where

where

• V_d is the potential applied across the plates and d is the separation.

The above equations indicate that in the region between the plates, the electron is accelerated upward, the velocity component v_y varying from point to point, whereas the velocity component v_x remains unchanged in the passage of the electron from one plate to another one. The path of movement of electron with respect to point O is readily known by combining Eqs. (3.14) and [3.15(b)], the variable t being eliminated.

This leads to the expression

The above equation indicates that the particle moves in a parabolic path in the region between the plates.