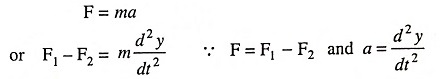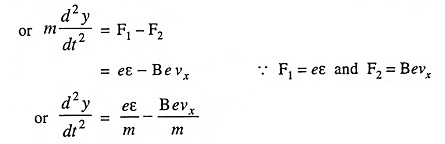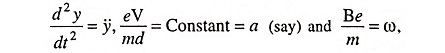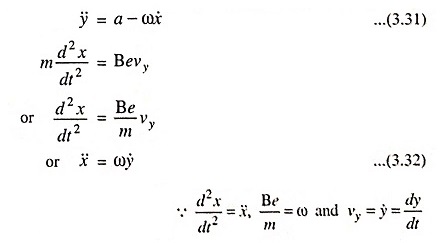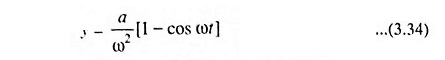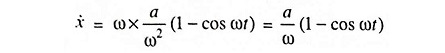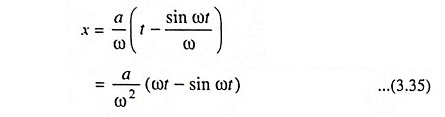Motion in Combined Electric and Magnetic Fields:

The Motion in Combined Electric and Magnetic Fields is given by the below two names, namely

• Parallel Electric and Magnetic Fields
• Perpendicular Electric and Magnetic Fields

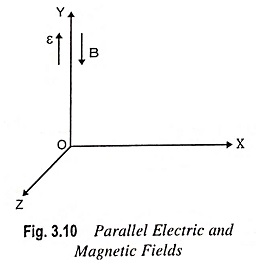
Parallel Electric and Magnetic Fields – If both electric and magnetic fields exist simultaneously, the fields being in same or opposite directions, and the initial  velocity of the electron is either zero or is directed along the fields, the magnetic field will have no effect on the electron. The resultant motion will depend solely upon the electric field intensity ε. It means that the electron will move in a direction parallel to the fields with a constant acceleration.

If the fields are chosen as illustrated in Fig. 3.10, the complete motion is given by

and

where

• a = eε/m is the magnitude of acceleration.

The negative sign is due to the fact that the direction of acceleration of an electron is opposite to the direction of electric field.

If, initially, a component of velocity v_ox perpendicular to the magnetic field exists, this component of velocity, together with the magnetic field, will result in circular motion, the radius of the circular path being independent of ε. However, electric field ε will cause change in velocity with time along the field. Thus, the resulting path will be helical with a pitch that changes with time. That is, the distance moved along the Y-axis per revolution increases with each revolution.

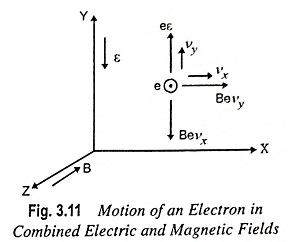
Perpendicular Electric and Magnetic Fields – An electron e is placed in the motion in combined electric and magnetic fields as shown in Fig. 3.11.

Assume that both e and B are perpendicular to each other. The initial velocity is zero, v_x and v_y are the velocities acquired by electron due to motion in combined electric and magnetic fields respectively.

According to Newton’s second law

where F₁ and F₂ are forces due to electric and magnetic fields respectively.

Substituting ε=V/d in above equation, we have

Since

the above equation becomes

Integrating above Eq. (3.32), we have

where C₁ is a constant of integration

From initial conditions C₁ = 0, therefore,

Substituting ẋ = ωy in Eq. (3.31), we have

Solving the above second order differential equation, we have

Substituting y = a/ω²[1-cosωt] in Eq. (3.33), we have

Integrating above equation, we have

The above equation is cycloidal.