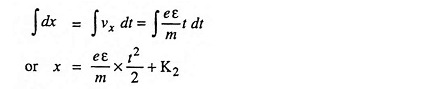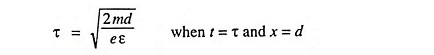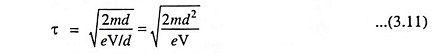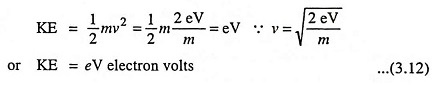Motion of Charged Particle in Electric Field:

Motion of Charged Particle in Electric Field – The electric field intensity which is equal to negative of the voltage gradient, is defined as the force (in newtons) acting per unit positive charge (in coulomb), and has the same direction as that of the force. Consequently, the force acting on a positive charge q placed in an electric field of intensity ε is given by qε the resulting force being in the direction of the electric field. Thus

where

• q = charge is in coulombs
• ε  = is in volts per metre.

Bold face type is used wherever vector quantities (those having both magnitude and direction) are encountered.

In order to calculate the path of a Motion of Charged Particle in Electric Field, the force, given by Eq. (3.4), must be related to the mass and the acceleration of the particle by Newton’s second law of motion. Hence

where

• m is the mass of charged particle in kg,
• a is acceleration in m/s² and
• v is velocity in m/s.

Comparing Eqs. (3.4) and (3.5), we have

The solution of above equation, subject to appropriate initial conditions, gives the path of the particle resulting from the action of the electric forces. If the magnitude of the charge on electron is e, the force on an electron in the field is

The minus sign denotes that the force is in the direction opposite the field.

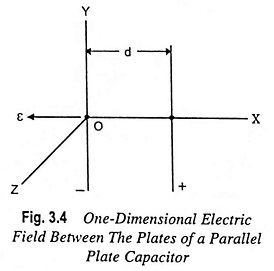
Now let us consider an electron situated between the two plates of a parallel plate capacitor contained in an evacuated envelope, as shown in Fig. 3.4. Pd is applied between the two plates, the direction of electric field in the region between the two plates being as shown. If the distance between the plates is small in comparison to the dimensions of the plates, the electric field may be considered to be uniform, the lines of force pointing along the negative X direction. It means that the only field that is present is ε along the -X axis.

Since there is no force along the Y or Z directions, according to Newton’s second law the acceleration along these axes must be zero. However, zero acceleration means constant velocity, and since the velocity is initially zero along these axes, the particle will not move along these axes. It means that the only possible motion is one-dimensional, and the electron moves along the X axis.

Thus, we have the motion of electron in X-direction with acceleration

where

• ε represents the magnitude of electric field.

Integrating above expression with respect to time, we have

At t = 0, the electron is at rest and the initial velocity of electron is zero. Hence the value of constant K₁ = 0. Thus, the expression for the velocity of the electron is

The velocity can also be written as

where

• x is the displacement of electron along -X axis.

Again integrating above expression with respect to time, we have

where

• K₂ is a constant of integration.

From initial conditions, when t = 0, x = 0, the electron being assumed to be at rest, therefore, K₂ = 0 and the expression for displacement of electron is

The above equation is for displacement x of the electron in accelerating electric field ε at time t, with initial velocity and displacement being zero.

Transit Time, τ. Transit time is defined as the time taken by an electron to travel a given distance.

From Eq. (3.10)

or the expression for transit time τ (time taken by electron to travel a distance d) is

Since ε = V/d where V is the potential difference applied across the plates of the parallel plate capacitor

So,

The kinetic energy (KE) possessed by the electron, when it reaches the other plate, at a distance d, under the influence of electric field ε is