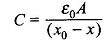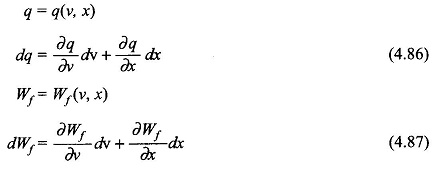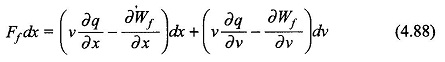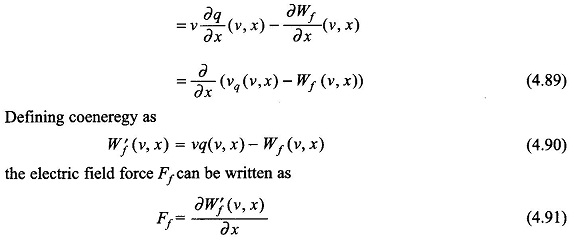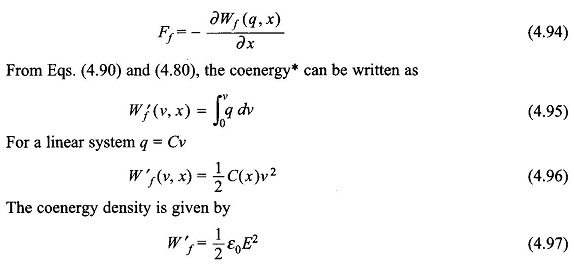Electromechanical Energy Conversion via Electric Field Energy:
Electromechanical energy conversion via the electric field is analogous to the magnetic field case studied earlier. Charge in the Electric Field Energy is analogous to flux linkages and voltage to current in the magnetic field case.
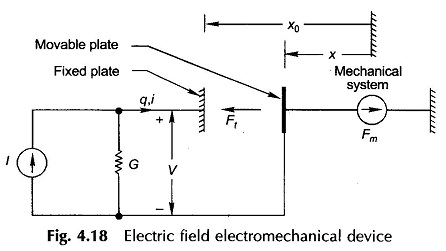
Figure 4.18 shows a parallel plate condenser with a fixed and a movable plate. The condenser is fed from a current source. The leakage current of the condenser is
represented outside by conductance so that the condenser’s electric field is conservative. Let us assume that the movable plate of the condenser is held fixed in position x. The electric energy input to the ideal condenser gets stored in the electric field so that
The capacitance C is a function of configuration (position x of the movable plate) and can be expressed as
where A= plate area and ε0 = permittivity of free space. Thus Wf, the field energy is a function of two independent variables q and x, i.e.
The expression of Eq. (4.82) for the field energy immediately reveals that the electric field can be changed electrically by changing q or mechanically by changing x, i.e. moving the movable plate.
The field energy can also be written as 
The energy density in the electric field can be expressed as
where
E = electric field intensity or potential gradient
Energy Conversion:
Let the movable plate of the device be now permitted to move under the action of the electric field force Ff As per the principle of energy conservation:
Mechanical energy output (work done by the field force) = electric energy input — increase in the field energy
![]() Let us choose (v, x) as independent variables. Then
Let us choose (v, x) as independent variables. Then
Substituting Eqs (4.86) and (4.87) in Eq. (4.85) and reorganizing
Since v and x are independent variables, the coefficient of dv in Eq. (4.88) must be zero. Hence