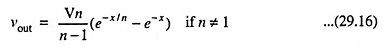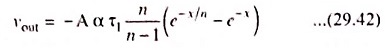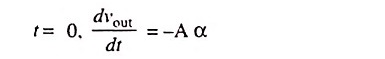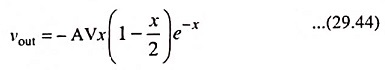Double Differentiation – Derivation:

Two R-C coupling networks in cascade separated by an ampli­fier A is shown in Fig. 29.36 (a). The amplifier A is to operate as a linear amplifier and the output impedance must be small with respect to the impedance of R₂ and C₂ so that this combination does not load the amplifier. Let R₁ be the parallel combina­tion of R and the input impedance of the am­plifier. The time constants R₁C₁ and R₂C₂ must be small in com­parison to the period of the input wave to en­able the circuit to per­form Double Differentiation.

When the input is a ramp (v_in = αt) of long duration, the output of the inverting amplifier is the negative of the wave­form shown in Fig. 29.10 (b) and is given by equation

where A is the magnitude of the amplifier gain and τ₁ is the time constant and is equal to R₁C₁. This exponential input to the net­work R₂C₂ in turn gives an output given by Eq. (29.16)

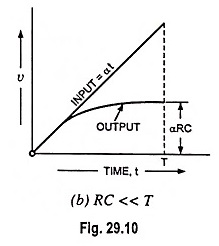
If n # 1 where n ≡ τ₂/τ₁, τ₂ = R₂C₂ and x ≡ t/τ₁, values of -v_out/Aατ₁ are plotted in Fig. 29.36 (b) for values of n equal to 0.1, 1.0, 10 and 100. For n = 1, the output is given by

This special case is plotted in Fig. 29.36 (c).

The noteworthy point is that a ramp voltage has been con­verted into a pulse. The initial slope of the output wave is the initial slope of the input multiplied by the amplifier gain. This is the reason that the stage in Fig. 29.36 (a) is known as “rate-of­-rise-amplifier”. For a single R-C circuit, the initial rate of change of output is equal to the initial rate of change of input independently of the time constant. Obviously, the same con­clusion can be arrived at for multiple differentiation. A direct check can be made from Eq. (29.42). where it is found that at

As a second illustration of Double Differentiation, we may consider the exponential waveform v_in = V(1 – e^-t/τ) applied to the circuit shown in Fig. 29.36 (a). For

τ₁ = τ₂ = τ

or R₁C₁ = R₂C₂ = τ, the output is found to be

where x = t/τ. This result is plotted in Fig. 29.36 (d). The initial slope of output voltage v_out is -AV/τ since V/τ is the initial slope of input voltage v_in. Also, direct integration reveals that the out­put waveform has as much area above the time axis as below, a fact of importance in some practical problems, such as in pulse spectrometry.