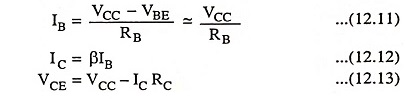Fixed Bias Circuit Diagram – Advantages and Disadvantages:

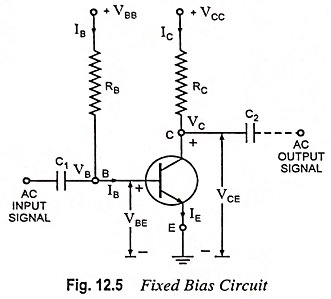
Fixed Bias Circuit Diagram shown in Fig. 12.5 uses two batteries V_BB and V_CC. The battery V_BB gives potential to the base terminal through resistance R_B (of the order of hundred kΩ) and battery V_CC supplies power to the collector through resistance R_C (of the order of kΩ).

The base current can be determined by applying Kirchhoff’s second law for the branch circuit, starting from battery V_BB to ground.

Since V_BE is very small (0.7 V in case of silicon transistor and 0.3 V in case of Ge transistor) in comparison to V_BB, not much error will be committed if it is neglected. The base current is then given by the simple expression

The supply voltage V_BB being of fixed value—once the resistance R_B is chosen—the base current I_B is also fixed. Hence the name fixed bias circuit is given.

The collector-emitter section consists of the supply battery V_CC, the collector resistor and the transistor collector-emitter junction. The currents through the collector and emitter are about the same since I_B is very small in comparison to either. For linear amplifier operation, the collector current will be β times base current, where β is the transistor current gain i.e.,

The base current I_B is determined from the operation of the base-emitter section of the circuit. The collector current, as shown above, will be β times the base current and not at all dependent on the resistance in the collector circuit. Thus collector current l_C is controlled by base-emitter section of the circuit.

Applying Kirchhoff’s second law to the branch circuit starting from V_CC to ground.

The quiescent point is given by I_C, V_CE.

The coupling capacitors C₁ and C₂ have reactances quite small at the frequency of ac signal, so that very little voltage drop of ac signal takes place across them. These capacitors are open circuit for direct currents, so that dc biasing potentials of this amplifier stage do not affect the circuits connected at the input as well as output terminals.

The fixed bias circuit is the simplest way to bias a transistor, but from stability point of view it is the worst circuit, because with the rise in temperature of transistor, β changes and also there is increase of leakage current and drop in V_BE value.

Since base current I_B controls the collector current I_C and I_C is equal to βI_B, with the change in the value of β, I_C changes (I_B remaining unchanged) and the operating point gets shifted.

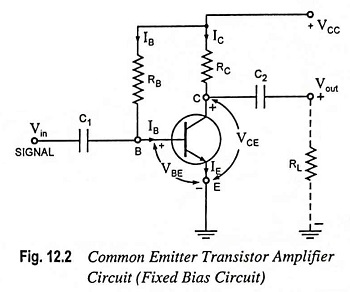
The circuit shown in Fig. 12.5 may be modified by using a single battery, as shown in Fig. 12.2. From the practical point of view, it is always preferable to have an electronic circuit operated from a single battery.

The expressions for I_B, I_C and V_CE are given below

Stability Factor S:

As we know from earlier section, the stability factor

and in Fixed Bias Circuit method I_B is independent of I_C, as obvious from Eq. (12.8) or Eq. (12.11), so stability factor is given as

If β = 150, then S = 151 which means that collector current I_C increases 151 times as much as I_CO. Such a large value of S makes thermal runaway, a definite possibility with this circuit.

Advantages and Disadvantages:

Though this biasing circuit is very simple, as very few components (only two resistors and one battery) are required, biasing conditions can be easily set, the calculations are simple and there is no loading of the source by the biasing circuit, as no resistor is used across base-emitter junction but this method of biasing is rarely used. This is due to the following reasons.

1. This method provides poor stability, as there is no means to stop a self increase in collector current I_C owing to temperature rise and individual variations. For example, if β increases either due to temperature rise or due to replacement of transistor, then collector current, l_C also increases by the same factor as base current I_B is constant.
2. There are good chances of thermal runaway. This is due to high stability factor S.