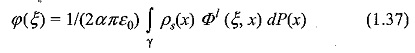Boundary Element Method (BEM) in Electric Field:
Though the charge simulation method is known for its accuracy and speed, it is not very efficient in case of multi-dielectric problems and very thin electrodes, which are often used to control and get the electric field strength in condenser bushings, transformers, etc. Such problems can be solved using the Surface Charge Simulation Method (SSM) which is also called Boundary Element Method (BEM).
In many cases, electrodes and insulators used in high voltage equipment consists of cylinders, spheres, cones, and plane electrodes. Therefore, it is necessary to consider elements having these shapes to achieve a realistic field simulation by using variable charge distribution on these surfaces. The elements are combined in computer code and used for the calculation of complex geometries wherever possible. Curved triangles are employed only at those positions where the above elements cannot be used. This method requires a large number of elements, normally more than 2000, independent of the surface shape and therefore leads to a very large number of system equations.
Principle of Boundary Element Method:
Principle of Boundary Element Method is very similar to CSM with area elements. Like in CSM, the BEM uses area charge elements to replace the real charges. However, BEM does not require that the system components should have actual symmetry. The discretization of the real charges is generally carried out by boundary elements having three or four nodes, which use linear shape functions to approximate the internal charge distribution. If the outer surface geometry is not covered, then suitable intermediate points can be added. BEM having predetermined shapes like cylinders, cones, spheres and toroids are available. The evaluation of the resulting potential functions of the Boundary Element Method is done by numerical integration.
Boundary Element Method Formulation:
Boundary Element Method Formulation calls for the scalar electric potential due to surface charge density, which is written as
where, φ1 denotes the fundamental solution of the potential problem, α = 1 or 2 for two or three-dimensional problems respectively, and ρs(x) denotes the surface charge density. Equation (1.37) is the basic equation for the source Formulation of the BEM. This equation can be solved using the standard point collocation procedure for discretized image charges that lie within the conducted boundaries. The collocation approach has been recognized as charge simulation. The electric field is then given by
The resulting system of equations obtained using the source formulation will again be asymmetric. By solving this system of equations, the unknown values of the charge density can be found. Once the charge distribution is known, potential and electric field values can be calculated throughout the domain using Eqs. (1.37) and (1.38) given above.