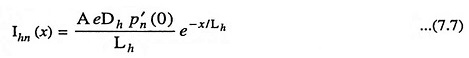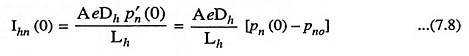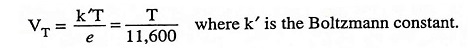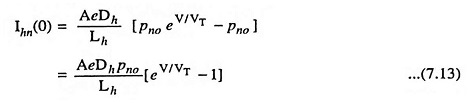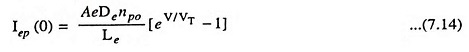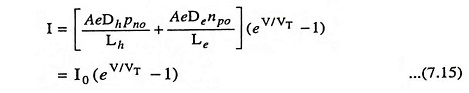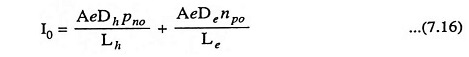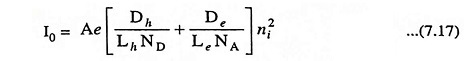Quantitative Theory of PN Junction Diode:

Quantitative Theory of PN Junction Diode – Here an expression for the total current will be derived as a function of the applied voltage with the assumption that depletion layer thickness is negligible (i.e., barrier width is zero).

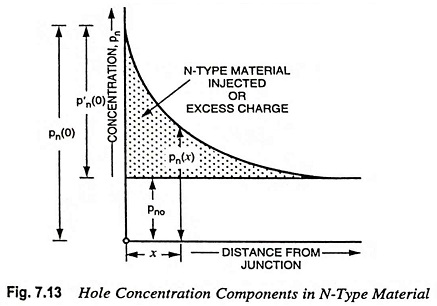
When a P-N diode is forward biased, holes are injected from P-region into the N-region. The concentration p_n of the holes in the N-region is increased above its thermal equilibrium value p_no. The hole concentration in N-region is given as

where p_no is the hole concentration in thermal-equilibrium condition, L_h is the diffusion length for holes in N-type material and x is the distance from the junction where concentration is considered.

The injected, or excess, concentration of holes at x = (0), p′_n(0) is given as

These several hole concentration components are shown in Fig. 7.13, which shows that the concentration p_n(x) falls exponentially with distance x into the N-type material.

The diffusion hole current in the N-region is given as

Taking the derivative of Eq. (7.4) and substituting the value of dp_n/dx in above Eq. (7.6), we have

At junction i.e., x = 0

where A is area of material in m², D_h is diffusion constant for holes in m²/s, e is the magnitude of charge on holes, L_h is the diffusion length of holes in N-type material in metre, and p′_n(0) is the excess of hole concentration at Quantitative Theory of PN Junction Diode.

Using Boltzmann relationship of kinetic theory of gases, we have

where V is the voltage applied across the P-N diode and V_T is the volt-equivalent of temperature and it is given as

The Eq. (7.9) is known as the law of junction.

Diffusion Length:

Diffusion length is defined as the distance travelled by free charge carriers (electrons or holes) before recombination. It may also be defined as the average distance covered by an excess charge carrier during its lifetime τ.

The diffusion length L_h and lifetime τ_h are related to each other as :

Similarly in case of P type semiconductor

Forward Currents:

The total diode current I at x = 0 is given as

where I_hn (0) is the current caused by holes entering the N-region and I_ep (0) is the current caused by electrons entering the P-region.

From Eqs. (7.8) and (7.9)

Similarly,

From Eqs. (7.12), (7.13) and (7.14) we have total diode current

where

Reverse Saturation Current:

In the foregoing discussion a positive value of V indicates a forward bias. Equation (7.15) is equally valid for reverse bias [i.e., for negative values of applied voltage V]. For a reverse bias voltage exceeding V_T (i.e., 26 mV) at room temperature (27 °C or 300 K), current I → – I₀. Thus I₀ is called the reverse saturation current.

The concentration of holes in N-type region,

The concentration of electrons in P-type region,

where N_D and N_A are the concentrations of donor and acceptor atoms respectively.

Substituting p_no = n²_i/N_D and n_po = n²_i/N_A  in Eq. (7.16), we have

where V_GO is a voltage numerically equal to the forbidden energy gap, E_GO in electron volts, and V_T is the volt equivalent of temperature and is equal to T/11,600.

For germanium the diffusion constants D_h and D_e vary approximately inversely proportional to temperature T. Hence I₀ may be given as

where K₁ is a constant, independent of temperature T.

In the discussion made above, the effect of carrier generation and recombination in the space-charge region has been ignored. Such an assumption is valid for a germanium diode (not for a silicon diode). For the silicon diode, a diffusion current is negligible in comparison with the transition-layer charge-generation current, which is given approximately by

where η ≈ 2 for small (rated) currents and η ≈ 1 for large currents.

Also I₀ is found to be proportional to n_i instead of n²_i so

where K₂ is a constant, independent of temperature T.