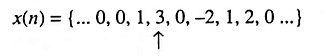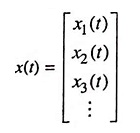Signal Definition and Classification of Signals:

A signal is a single valued function of one or more variables that conveys some information. Signals are represented mathematically as the functions of one or more independent variables. A signal may be a function of time, temperature, position, pressure, distance etc. In electrical sense, the signal can be voltage or current. The voltage or current is the function of time as an independent variable.  The Classification of Signals are namely

1. The signals can be one-dimensional or multidimensional.

• One-Dimensional Signals: When the function depends on a single variable, the signal is said to be one dimensional. Speech signal, whose amplitude varies with time, is one-dimensional signal.
• Multidimensional Signals: When the function depends on two or more variables, the signal is said to be multidimensional signal. Image is an multidimensional signal because it is a two-dimensional signal with horizontal and vertical coordinates.

2. Based upon their nature and characteristics in the time domain, the signals may be broadly classified as given below:

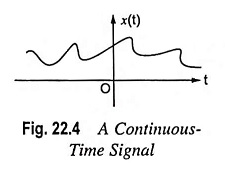
• Continuous-Time Signals: This function is defined continuously in the time domain. A continuous-time signal is represented by x(t) where x represents the shape of the signal and t shows that the variable is time. This signal will have some value at every instant of time. Figure 22.4 shows a continuous-time signal.

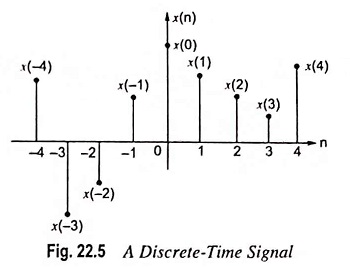
• Discrete-Time Signals: A discrete-time signal is defined only at certain time-instants. For discrete-time signals, the amplitude between two time instants is not defined. It is represented by x(n), here time n is the independent variable. Figure 22.5 shows a discrete-time signal. Mathematically, a discrete-time signal is denoted as under:

Here arrow indicates the value of x(n) at n = 0.

3. Real and Complex Signals: A signal x(t) is a real signal if its value is a real number. Similarly, a signal x(t) is a complex signal if its value is a complex number.

4. Deterministic and Non-Deterministic (Random) Signals: Deterministic signals are those signals which can be completely specified in time. The pattern of this type of classification of signals is regular and can be characterized mathematically. Also, the nature and amplitude of such a signal at any time can be predicted. So these signals are called deterministic signals.

A non-deterministic signal is one whose occurrence is always random in nature. The pattern of such a signal is quite irregular so these signals are also called random signals. For example, a thermal noise generated in an electric circuit is a non-deterministic signal.

5. Periodic and Non-Periodic Signals:

• Periodic Signal: A signal which repeats itself after a fixed time period is called a periodic signal. It can be defined mathematically as

x(t) = x(t + T₀). It is a condition of periodicity.

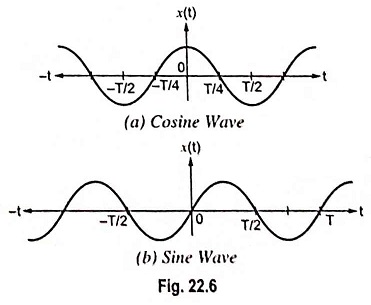
Here T₀ is called as the period of signal x(t). Example of these signals are sine wave, cosine wave, square wave etc.

• Periodic Discrete-Time Signal: For the discrete-time signal, the condition of periodicity is

x(n) = x(n + N)

Here, N is the period of signal and its smallest value is called as fundamental period.

• Non-Periodic Signal: A signal which does not repeat itself after a fixed time period or does not repeat at all is called as non-periodic or aperiodic signal. Mathematical expression for this signal is

x(t) ≠ x(t + T₀)

Sometimes value of period T₀ = ∞ then it is an exponential signal and mathematically can be expressed as

x(t) = e^-αt

• Non-Periodic Discrete-Time Signal: Mathematical expression for this classification of signals is,

x(n) ≠ x(n + N)

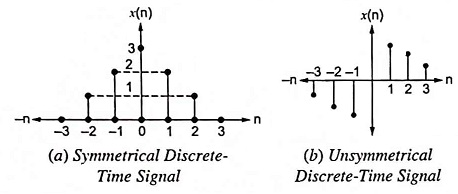
6. Symmetrical (Even) or Anti symmetrical (Odd) Signals:

• Symmetrical Continuous Time Signal: A signal x(t) is symmetrical or even if it satisfies the following condition:

x(t) = x(-t)

Here x(t) is value of signal for positive t and x(-t) is value of signal for negative t. Cosine wave is an example of symmetrical continuous time signal.

• Antisymmetrical Continuous Time Signal: A signal x(t) is antisymmetrical or odd if it satisfies the following condition:

x(t) = -x(-t)

Sine wave is an example of antisymmetrical continuous time signal.

• Symmetrical Discrete-Time Signal: This type of classification of signals satisfies the following condition and is shown in Fig. 22.7(a).

x(n) = x(-n)

• Unsymmetrical Discrete-Time Signal: This type of classification of signals satisfies the following condition and is shown in Fig. 22.7(b).

x(n) = -x(-n)

7. Energy and Power Signals: Signals may be classified as energy and power signals. However, there are some signals which can neither be classified as energy signals nor power signals.

The energy signal is one which has finite energy and zero average power.

x(t) is an energy signal if it satisfies following condition:

0 < E < ∞ and P = 0

Here, E is the energy and P is the power of signal x(t). The power signal is one which has finite average power and infinite energy.

x(t) is a power signal if it satisfies following condition:

0 < P < ∞ and E = ∞

8. Single Channel and Multichannel Signals: Multichannel signals are generated by multiple sources or multiple sensors. The resultant signal is the vector sum of signals from all channels. It is expressed as:

A common example of multichannel signal is ECG waveform.

9. One-Dimensional and Multidimensional Signals: If a signal is a function of single independent variable, the signal is called as one-dimensional signal. On the other hand, if the signal is a function of multi independent variables then it is called as multidimensional signal.

For example, to locate a pixel on the TV screen, two coordinates X and Y are required and this pixel is a function of time too. This it is a multidimensional signal and can be expressed mathematically as P(x, y, t).