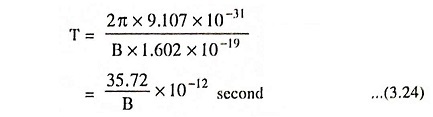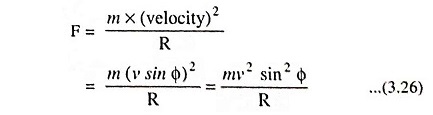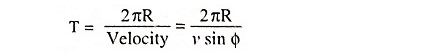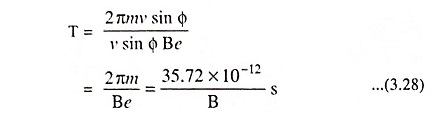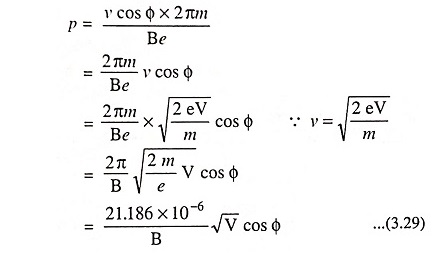Motion of an Electron in a Magnetic Field:
Motion of an Electron in a Magnetic Field – Consider an electron to be placed in the region of magnetic field. If an electron is at rest, the force experienced by the particle, Fm = 0 and the particle remains at rest.
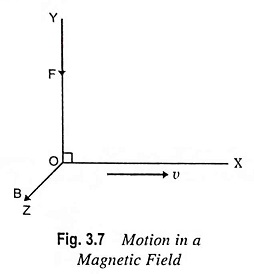
If an electron moves parallel to the field, no force is experienced by it (Fig. 3.7). Thus, a particle whose initial velocity has no component normal to a uniform magnetic field will continue to move with constant speed along the lines of flux.
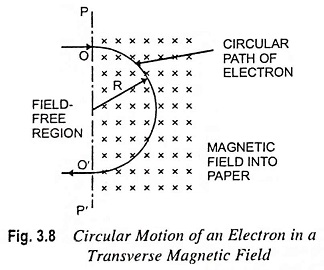
Now consider an electron moving with a speed v to enter a constant uniform magnetic field normally, as illustrated in Fig. 3.8. Since the force experienced due to magnetic field Fm is perpendicular to v and so to the motion at every instant, the work done on electron is zero. This means that its kinetic energy is not increased, and so its speed remains unaltered. Further, since v and B are each constant in magnitude, then Fm is constant in magnitude and perpendicular to the direction of motion of the particle. This type of force results in motion in a circular path with constant speed.
For determination of the radius of the circle, it is recalled that a particle moving in a circular path with a constant speed v has an acceleration toward the centre of the circle of magnitude v2/R, where R is the radius of path in metres. Then
From above relation, we have
The corresponding angular velocity in radians per second is
The time in seconds for one complete revolution, known as the period, T is given by
For an electron, this reduces to
In these equations, e/m is in coulombs/kg and B is in webers/m2.
As the radius of the path is directly proportional to speed [Eq. (3.21)], faster moving particles will traverse large circles in the same time that a slower particle moves in its smaller circle.
This theory is the basis of operation of numerous devices such as cyclotron and magnetic focusing apparatus.
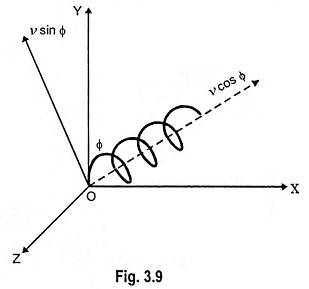
If the initial velocity makes an angle Φ with the field, the trajectory of an electron is a helix, as illustrated in Fig. 3.9.
v cos Φ is the component along the axis of B and v sin Φ is the component perpendicular to B, and therefore, the force due to component v cos Φ is zero. The force due to v sin Φ component is
Also
Comparing Eqs. (3.25) and (3.26), we have
Also, period of rotation,
Substituting R = mv sin Φ/Be in above equation, we have
The pitch of the helix (distance travelled along the direction of B in one revolution).
Substituting T = 2πm/Be in above equation, we have