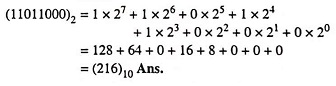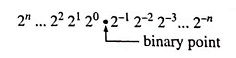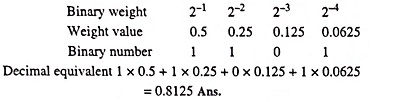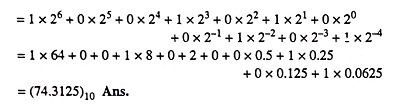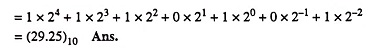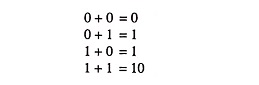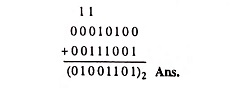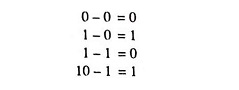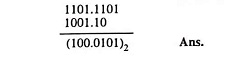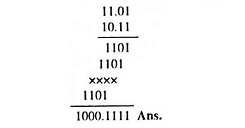Binary Number System (Definition, Conversions & Examples):
The binary number system is simply another way to count. It is less complicated than the decimal number system because it is composed of only two digits 0 and 1. Just as the decimal system with its ten digits is a base-10 system, the binary system with its two digits is a base-2 system. These two digits namely 0 and 1 carry the same meaning as in the decimal system but different meaning is given to the position occupied by the numeral or digit. In a binary system, the base is 2, so any number can be expressed by an array of numerals representing the coefficients of power of 2 and not 10. In a binary system, the weight of each successively higher position (to the left) is an increasing power of 2.
Counting in Binary:
To learn to count in binary, let us first look how we count in decimal number system. We start counting from 0, 1, 2, 3 and up to 9. After 9 we write 0 with 1 on its left side i.e., 10. Now we have two digit number. To continue counting, first digit of number i.e., 0 is again changed up to 9 and after that it is written 0 and second digit of number (which was earlier 1) is written 2. Thus we get number 20. This way we count the number up to 99. In further counting the number digit 99 is changed to 00 with digit 1 on the left side of these digits added. So we get number 100. This is the way of counting and writing down the numbers in decimal number system.
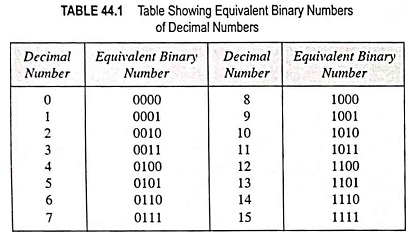
A comparable situation occurs when counting in binary, except that we have only two digits. Counting is started with zero and ended with next number 1. After 1 there is no other digit in this system so in further counting, digit 1 is replaced by 0 with digit 1 on its left side i.e., 10. Next number follows 11. Again after number 11 digit 00 is written with digit 1 on the left side i.e., 100. This way we count in binary system. Table 44.1 shows the equivalent binary numbers of decimal numbers from 0 to 15. This Table 44.1 makes us more clear about binary number system.
Some terms like bit, nibble and byte are used in binary number system. Bit is used for a single binary digit. A binary number with four bits is called a nibble. When binary number has eight bits, then it is called a byte. Binary numbers have numerous advantages in digital computer’s use.
- An ordinary switch has two states either open or close which can be used to represent binary numbers.
- When current flows through a wire, magnetic flux is created across the wire. Direction of flux depends upon the direction of flow of current which can be determined by right hand rule. As the current can flow either in outward or in inward direction and, therefore, flux created would be either in counter-clockwise or clockwise direction so a magnetic core can be used to represent binary numbers, because of its two state operation. In earlier computers, thousands of magnetic cores were used to store the binary instructions and data.
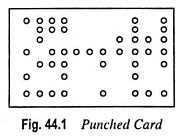
- A card with punched holes can also be used to represent the binary numbers. A card has two states, one state is without punching and the other is with punched holes in it. So it is a two-state device. Binary data and instructions, are stored in the card with the help of a card punching machine which punches the card in a prearranged code, as shown in Fig. 44.1.
- Like the punched card, a magnetic tape may also be used as a two state device. Some points of magnetic tape are magnetized while leaving other points unmagnetized. A row of the points represents data or instructions. So a magnetic tape reel can be used to store thousands of binary data and instructions.
- Use of transistor as two state device has already been discussed. Two states of transistors i.e., cutoff and saturation are used to produce an output of a transistor either low or high.
Binary-To-Decimal Conversion:
The binary number system is a positional system where each binary digit (bit) carries a certain weight based on its position relative to the least significant bit (LSB). The right-most bit is the LSB in a binary number and has a weight of 20 = 1. Any number can be converted to its decimal equivalent simply by adding the products of each bit and its weight. For example
Example 44.5: Find the decimal equivalent of binary number 11010.
Solution:
Example 44.6: Obtain the following: Decimal equivalent to (11011000)2.
Solution:
Binary Fractions:
So far, we have discussed binary integers (whole numbers). Fractional numbers can also be represented in binary by placing bits to the right of the binary point, just as fractional decimal digits are placed to the right of the decimal point.
The column weights of a binary number are
This indicates that all the bits to the left of the binary point have weights that are positive powers of two, as previously mentioned, but all bits to the right of the binary point have weights that are negative power of two, or fractional weights (2-1 = 1/21 etc.).
Binary fractional number can also be converted into decimal fractional numbers. Let us take, for example, a binary fractional number 0.1001.
It can also be written as
0.1001 = 1 (2-1) + 0 (2-2) + 0 (2-3) + 1 (2-4)
and after solving the above equation, we get
0.1001 = 1(0.5) + 0(0.25) + 0(0.125) + 1(0.0625) = 0.5625
So decimal equivalent of binary fractional number 0.1001 is 0.5625.
Mixed binary number can be converted into a decimal number by converting integer binary number and fractional binary number individually as described above.
Example 44.7: Convert the binary fractional number 0.1101 into its decimal equivalent.
Solution:
Example 44.8: Convert the following number into decimal (1001010.0101)2.
Solution: (1001010.0101)2
Example 44.9: Convert 11101.01 to decimal.
Solution: (11101.01)2
Decimal-To-Binary Conversion:
For the conversion of a decimal number into a binary number, decimal number is divided by 2 progressively and remainder is written down after each division. The remainder is then taken in a reverse order and it is the binary equivalent. This method of conversion is usually called the double dabble method.
Let us, for example, convert decimal number 19 into binary number to make above method clear.
In this last division remainder is 1. Now write down all remainders in reverse order to get binary equivalent of decimal number 19. So binary equivalent is 10011.
Fractional decimal numbers are converted into binary numbers, multiplying it by 2. Carry in the integer position of the result is recorded and carry of the decimal position is again multiplied by 2. Again the process is repeated. The carries of integer position recorded are written downward, which gives fractional binary number equivalent of fractional decimal number.
Let us, for example, convert fractional decimal number 0.65 into fractional binary number to make the method described above clear.
Now write down all the carries downward. It gives fraction binary number 0.10100110. Thus equivalent fraction binary number of 0.65 is 0.10100110.
In above conversion we stopped after eight binary digits and, therefore, this result is approximate. We can continue multiplying by 2 until we get as many digits as necessary for our application in order to have required accuracy.
Example 44.10: Convert (1245)10 into binary number system.
Solution:
Binary Operations:
We are familiar with the arithmetic operations such as addition, subtraction, multiplication and division in a decimal number
system. Similar operations can be performed on binary numbers, infact, binary arithmetic is much simpler than decimal arithmetic because here only two digits, 0 and 1 are involved.
In binary number system, addition is the most important of the four operations of addition, subtraction, multiplication and division. By using ‘complements’, subtraction can be reduced to addition. Most digital computers subtract by complements. It leads to reduction in hardware because circuitry is required only for addition operation. Similarly, multiplication is nothing but repeated addition and, finally division is nothing but repeated subtraction.
Binary Addition:
One method of addition of binary numbers is to convert binary numbers into decimal numbers, add them and then again convert the resultant decimal number into binary number. But this method is very time consuming and, therefore, we would discuss the direct and time saving method.
There are four cases, described below for addition of binary numbers.
With the help of the above four cases, all binary numbers can be added.
Let us, for example, add two binary numbers 10010 and 11011.
Now in this case first of all least significant digits of binary numbers are added. These digits are 0 and 1. We know that addition of 0 and 1 gives us 1. So in first column we write 1
Example 44.15: Complete the following operation 00010100 + 00111001 = ( )2.
Solution:
Binary Subtraction:
Again for subtraction of binary numbers, four cases are required to be considered while subtracting
Let us, for example subtract binary number 1001 from binary number 1010.
First of all least significant column is taken for subtraction. In this case 1 is to be subtracted from zero. So 1 is borrowed from the next column of binary number 1010. Now subtraction of 1 from 10 gives 1
So
Example 44.17: Perform the following binary operation (1101.1101)2 – (1001.10)2
Solution:
Binary Multiplication:
Multiplication is performed in binary in the same way as with decimal numbers. It involves forming the partial products, shifting each successive partial product left one place, and then adding all the partial products. The four simple rules are as follows:
Example 44.18: will illustrate the procedure.
Example 44.18: Perform the arithmetic operation 11.01 x 10.11.
Solution:
Binary Division:
Binary division is obtained as decimal division. Following example will illustrate the procedure.
Example 44.19: Perform the arithmetic operation indicated (11101101)2 /(11101)2 = (?)2
Solution:
Shifting a Number To Left or Right:
As in a decimal number system shifting one step to the left or right corresponds respectively to multiplication or division by 10, similarly shifting binary numbers one step to the left or right corresponds respectively to multiplication or division by 2.
When binary number 111002 corresponding to decimal number 28 is shifted one step to the left, it becomes 1110002 which corresponds to decimal number 56 i.e., it is doubled. If the given number is shifted one step to the right it becomes 11102 which corresponds to decimal number 14, i.e., it is halved.
Shifting The Place Point:
As in a decimal number system, moving of a decimal point one place to the right or left corresponds respectively to multiplication or division by 10, similarly shifting the binary point by one place to the right or left multiplies or divides by 2. For example 1011.02 corresponds to (11)10 but 101102 corresponds to (22)10 while (101.1)2 corresponds to (5.5 )10.