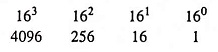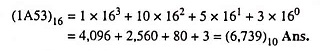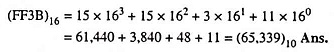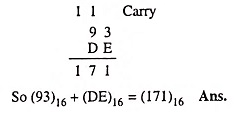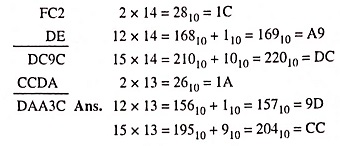Hexadecimal Number System (Definition, Conversions & Examples):
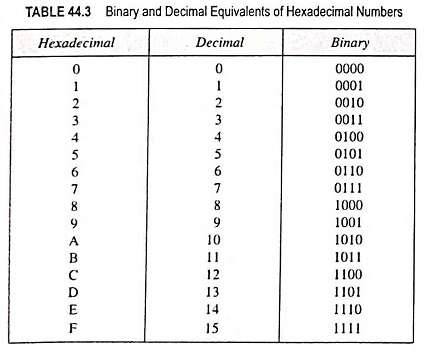
The binary number system forms the natural choice for the two-state systems. But in this system, the numbers tend to get short rather long. Hence to reduce the length of a given number it is quite common to use hexadecimal system. The hexadecimal number system has a base of 16 : that is, it is composed of 16 digits and characters. It uses the digits 0 through 9 plus the letters A, B, C, D, E and F. Since numeric digits and alphabets both are used to represent the digits in the hexadecimal number system, this is an alphanumeric number system. Table 44.3 shows the relationship between hexadecimal, decimal and binary. It is important to note that hex (abbreviation for hexadecimal) digits A through F are equivalent to the decimal values 10 through 15.
From the Table 44.3, it is observed that there are 16 combinations of 4-bit binary numbers and sets of 4-bit binary numbers can be entered in the computer in the form of hexadecimal (hex) digits. These numbers are required to be converted into binary representations using hexadecimal-to-binary converter circuits before these can be processed by the digital circuits. This system is extensively used in microprocessor work.
Counting in Hexadecimal:
How do we count in hexadecimal number system once we get to F ? Simply start over with another column and continue as follows:
With two hexadecimal digits, we can count up to FF16, which is equal to 25510. For counting beyond this, three hexadecimal digits are required. For instance, 10016 is equal to 25610, 10116 is equal to 25710 and so forth. The maximum three-digit hexadecimal number is FFF16 which is equal to 409510.
Hexadecimal-To-Decimal Conversion:
A hexadecimal number can be converted to its decimal equivalent by multiplying each hex digit by its weight and then taking the sum of these products. The weights of a hex number are increasing powers of 16 (from right to left). For a four-digit hex number the weights are as follows:
For illustration let us consider some examples.
Example 44.41: Find the decimal equivalent of hex number 1A53.
Solution:
Example 44.42: Convert (FF3B)16 to equivalent decimal.
Solution:
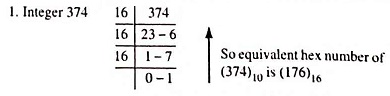
Decimal-To-Hexadecimal Conversion:
Repeated division of a decimal number by 16 will produce the equivalent hex number formed by the remainder of each division. This is similar to the repeated division by 2 for decimal-to-binary conversion and repeated division by 8 for decimal-to-octal conversion. Following examples illustrate the procedure.
Example 44.44: Convert the following number: (374.37)10 = ( )16
Solution:
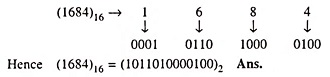
Hexadecimal-To-Binary Conversion:
Hex numbers can be converted into equivalent binary numbers by replacing each hex digit by its equivalent 4-bit binary number. This procedure is illustrated below.
Example 44.46: Do the following conversion: (1684)16 to ( )2
Solution:
Example 44.47: Convert the following number (A6B.F5)16 → (?)2.
Solution: Converting each hexadecimal digit to binary number of bit we have
Binary-To-Hexadecimal Conversion:
Conversion from binary to hex is just the reverse of the process above. The binary number is grouped into groups of 4-bits starting from LSB and moving towards MSB for integer part and then each group of four bits is replaced by its hex representation. Zeros are added, as required to complete a 4-bit group.
For the fractional part, the above procedure is repeated from the bit next to the binary point and moving towards the right.
Example 44.49: Convert the long binary number 1001001101010001 to octal and to hexadecimal.
Solution: (1001001101010001)2
Conversion From Hex-To-Octal and Vice versa.
Hexadecimal numbers can be converted to equivalent octal numbers and octal numbers can be converted to equivalent hex numbers by converting the hex/octal number to equivalent binary and then to octal/hex respectively. The procedure is illustrated by the following example.
Example 44.50: Convert (F2A4)16 into ( )8.
Solution: (F2A4)16
Example 44.51: Convert Hexadecimal number A5F1 to equivalent octal number.
Solution:
Hexadecimal Arithmetic:
The rules for arithmetic operations with hex numbers are similar to the rules for decimal, octal and binary numbers. The information can be handled only in binary form in a digital circuit and it is convenient and easier to enter the information using hex numbers. Since arithmetic operations are performed by the digital circuits on binary numbers, hex numbers are to be first converted into binary numbers. Following few examples illustrate the procedure.
Example 44.56: Find the hex sum (93)16 + (DE)16
Solution:
Example 44.58: Perform indicated operation FC216 x DE16 = ?
Solution:
Example 44.59: Divide 1EC8716 by A516.
Solution: