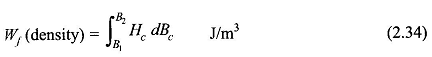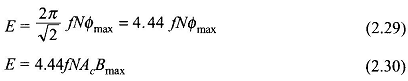Energy Density Formula in Magnetic Circuit:
The Energy Density Formula of transformers, ac machines and several other electromagnetic devices are excited from ac rather than dc sources. With ac operation, inductance is effective even in steady-state operation. Often, the flux is determined by the impressed voltage and frequency, and the magnetization current has to adjust itself in accordance with the flux so that B-H relationship is satisfied.
Except when linearity is desirable, economic utilization of material demands that working flux density should lie in the nonlinear zone (but not in the region of deep saturation). Exact and accurate analysis, therefore, cannot be predicted on the basis of constant inductance. Still circuit models (equivalent circuits) with constant parameters are often used. It will be seen in later chapters that these not only provide simplified approach but at the same time yield the desired accuracy for engineering applications.
Consider the N-turn iron-core coil of Fig. 2.1. Complete linearity of the magnetic circuit will be assumed. Magnetic flux Φ is produced by the exciting current i. Let the current and so the flux vary sinusoidally with time. Then
The induced emf in the coil as per Faraday’s law (Eq. (2.17)) is
and its rms value is
where Bmax is the maximum value of the flux density and Ac is the core’s area of cross-section.
The polarity of the emf must, in accordance with Lenz’s law, oppose the flux change and, therefore, is as shown in Fig. 2.1 when the flux is increasing. Since the current produces the flux instantaneously and in proportion to it (quasi-static field), they are in phase. From Eqs. (2.27) and (2.28), it is found that the induced emf leads the flux (hence the current) by 90°. The induced emf and coil resistance drop oppose the impressed voltage. However, resistance drop in many ac electromagnetic devices is quite small and may be neglected to a close approximation.
The electric power input into the magnetic circuit of Fig. 2.1 through the coil terminals is
The electric energy input which gets stored in the magnetic field in the time interval t1 to t2 is
where Wf = increase in field energy as the coil flux linkages change from λ1 to λ2 In field quantities
wherein Aclc is the volume of the core. Thus the Energy Density Formula in the field is given by