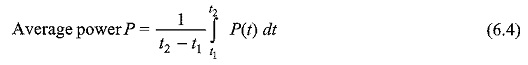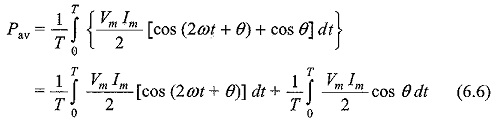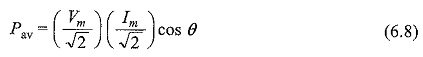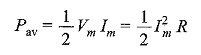Average Power Formula:

To find the average value of any power function, we have to take a particular time interval from t₁ to t₂; by integrating the function from t₁ to t₂ and dividing the result by the time interval t₂ — t₁, we get the Average Power Formula.

In general, the average value over one cycle is

By integrating the instantaneous power P(t) in Eq. 6.5 over one cycle, we get average power

In Eq. 6.6, the first term becomes zero, and the second term remains. The average power is therefore

We can write Eq. 6.7 as

In Eq.6.8, V_m/√2 and I_m/√2 are the effective values of both voltage and current.

To get average power, we have to take the product of the effective values of both voltage and current multiplied by cosine of the phase angle between voltage and the current.

If we consider a purely resistive circuit, the phase angle between voltage and current is zero. Hence, the average power is

If we consider a purely reactive circuit (i.e. purely capacitive or purely inductive), the phase angle between voltage and current is 90°. Hence, the average power is zero or P_av = 0.

If the circuit contains complex impedance, the average power is the power dissipated in the resistive part only.