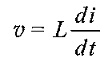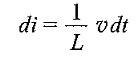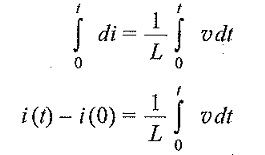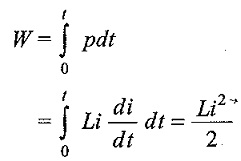Inductance Formula | Inductance Symbol:
Inductance Formula explains that when a wire of certain length, when twisted into a coil becomes a basic inductor. If current is made to pass through an inductor, an electromagnetic field is formed. A change in the magnitude of the current changes the electromagnetic field. Increase in current expands the fields, and decrease in current reduces it. Therefore, a change in current produces change in the electromagnetic field, which induces a voltage across the coil according to Faraday’s law of electromagnetic induction.
The unit of inductance is henry, denoted by H. By Inductance Formula, the inductance is one henry when current through the coil, changing at the rate of one ampere per second, induces one volt across the coil.
Inductance Symbol:
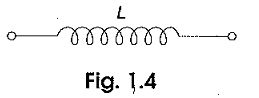
The inductance symbol is shown in Fig. 1.4.
Inductance Formula in terms of Voltage and Current:
The current voltage relation is given by ,
where
- v is the voltage across inductor in volts, and
- i is the current through inductor in amps.
we can rewrite the above equations as
Integrating both sides, we get
From the above equation we note that the current in an inductor is dependent upon the integral of the voltage across its terminals and the initial current in the coil, i(0).
The power absorbed by inductor is
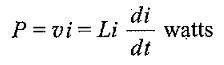The energy stored by the inductor is
From the above discussion, we can conclude the following.
- The induced voltage across an inductor is zero if the current through it is constant. That means an inductor acts as short circuit to dc.
- A small change in current within zero time through an inductor gives an infinite voltage across the inductor, which is physically impossible. In a fixed inductor the current cannot change abruptly.
- The inductor can store finite amount of energy, even if the voltage across the inductor is zero, and
- A pure inductor never dissipates energy, only stores it. That is why it is also called a non-dissipative passive element. However, physical inductors dissipate power due to internal resistance.