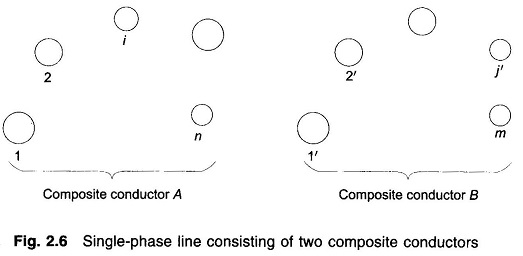
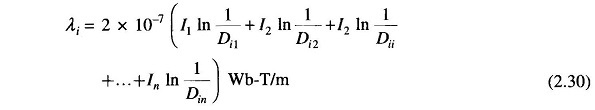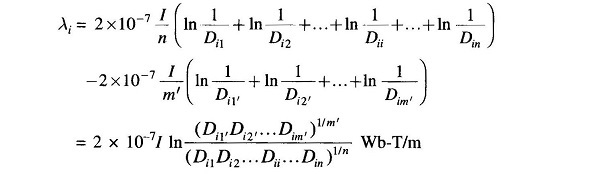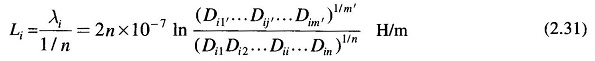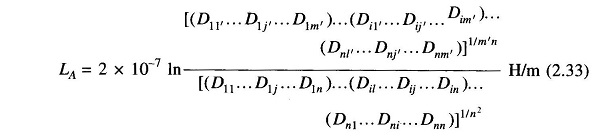Inductance of Composite Conductor Lines:
Future 2.6 shows such a single-phase line comprising inductance of composite conductor lines A and B with A having n parallel filaments and B having m’ parallel filaments. Though the inductance of each filament will be somewhat different (their resistances will be equal if conductor diameters are chosen to be uniform), it is sufficiently accurate to assume that the current is equally divided among the filaments of each inductance of composite conductor lines. Thus, each filament of A is taken to carry a current I/n, while each filament of conductor B carries the return current of — I/m’.
Applying Eq. (2.30) to filament i of conductor A, we obtain its flux linkages as
The inductance of filament i is then
The average inductance of the filaments of composite conductor A is
Since conductor A is composed of n filaments electrically in parallel, its inductance is
Using the expression for filament inductance from Eq. (2.31) in Eq. (2.32), we obtain
The numerator of the argument of the logarithm in Eq. (2.33) is the m′nth root of the m′n terms, which are the products of all possible mutual distances from the n filaments of conductor A to m’ filaments of conductor B. It is called mutual geometric mean distance (mutual GMD) between conductors A and B and is abbreviated as Dm. Similarly, the denominator of the argument of the logarithm in Eq. (2.33) is the n2th root of n2 product terms (n sets of n product terms each). Each set of n product term pertains to a filament and consists of r′(Dii) for that filament and (n-1) distances from that filament to every other filament in conductor A. The denominator is defined as the self geometric mean distance (self GMD) of conductor A, and is abbreviated as DsA. Sometimes, self GMD is also called geometric mean radius (GMR).
In terms of the above symbols, we can write Eq (2.33) as
Note the similarity of the above relation with Eq. (2.22b), which gives the inductance of one conductor of a single-phase line for the special case of two solid, round conductors. In Eq. (2.22b) r’1 is the self GMD of a single conductor and D is the mutual GMD of two single conductors.
The Inductance of Composite Conductor Lines B is determined in a similar manner, and the total inductance of the line is