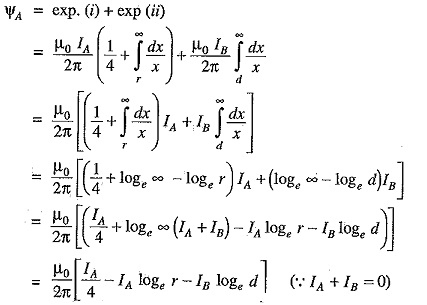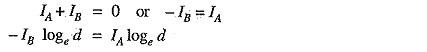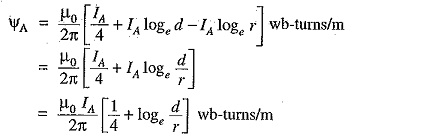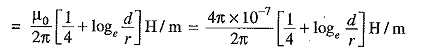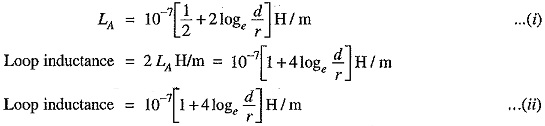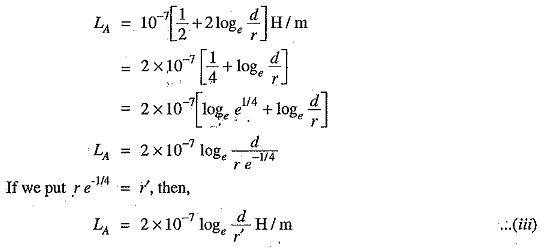Inductance of Single Phase Two Wire System:
A Inductance of Single Phase Two Wire System consists of two parallel conductors which form a rectangular loop of one turn. When an alternating current flows through such a loop, a changing magnetic flux is set up. The changing flux links the loop and hence the loop (or single phase line) possesses inductance. It may appear that inductance of a single phase line is negligible because it consists of a loop of one turn and the flux path is through air of high reluctance. But as the X -sectional area of the loop is very large, even for a small flux density, the total flux linking the loop is quite large and hence the line has appreciable Inductance of Single Phase Two Wire System.
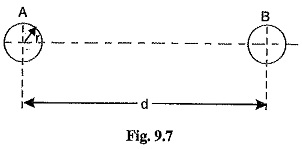
Consider a single phase overhead line consisting of two parallel conductors A and B spaced d metres apart as shown in Fig. 9.7. Conductors A and B carry the same amount of current (i.e. IA = IB), but in the opposite direction because one forms the return circuit of the other.
In order to find the inductance of conductor A (or conductor B), we shall have to consider the flux linkages with it. There will be flux linkages with conductor A due to its own current IA and also due to the mutual inductance effect of current IB in the conductor B.
Flux linkages with conductor A due to its own current
Flux linkages with conductor A due to current IB
Total flux linkages with conductor A is
Inductance of conductor A,
Note that eq.(ii) is the Inductance of Single Phase Two Wire System and is sometimes called loop inductance. However, inductance given by eq.(i) is the inductance per conductor and is equal to half the loop inductance.
Expression in alternate form: The expression for the inductance of a conductor can be put in a concise form.
The radius r′ is that of a fictitious conductor assumed to have no internal flux but with the same inductance as the actual conductor of radius r. The quantity e-1/4 = 0.7788 so that
The term r′ (= r e-1/4) is called geometric mean radius (GMR) of the wire. Note that eq.(iii) gives the same value of inductance LA as eq.(i). The difference is that eq.(iii) omits the term to account for internal flux but compensates for it by using an adjusted value of the radius of the conductor.
Note that r′ = 0.7788 r is applicable to only solid round conductor.