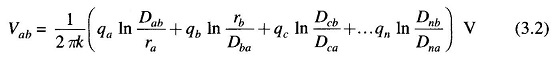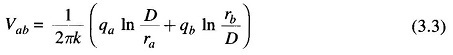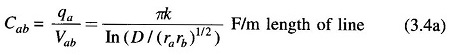Capacitance of Two Wire Line:

Consider a Capacitance of Two Wire Line shown in Fig. 3.3 excited from a single-phase source. The Capacitance of Two Wire Line develops equal and opposite sinusoidal charges on the two conductors which can be represented as phasors q_a and q_b so that q_a = – q_b.

The potential difference V_ab can be written in terms of the contributions made by q_a and q_b by use of Eq. (3.2) with associated assumptions (i.e. D/r is large and ground is far away). Thus,

Since

The line capacitance C_ab is then

or

If r_a = r_b = r,

The associated line charging current is

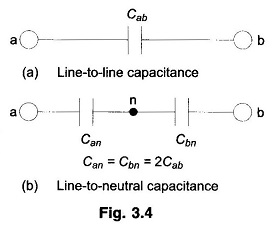
As shown in Figs. 3.4 (a) and (b) the line-to-line capacitance can be equivalently considered as two equal capacitances is series. The voltage across the lines divides equally between the capacitances such that the neutral point n is at the ground potential. The capacitance of each line to neutral is then given by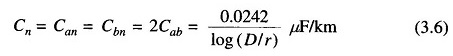

The assumptions inherent in the above derivation are:

1. The charge on the surface of each conductor is assumed to be uniformly distributed, but this is strictly not correct.

If non-uniformity of charge distribution is taken into account, then

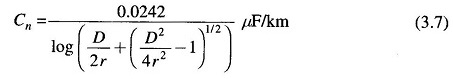
If D/2r ≫ 1, the above expression reduces to that of Eq. (3.6) and the error caused by the assumption of uniform charge distribution is negligible.

2. The cross-section of both the conductors is assumed to be circular, while in actual practice stranded conductors are used. The use of the radius of the circumscribing circle for a stranded conductor causes insignificant error.