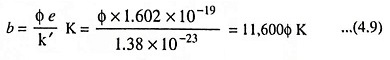What is Thermionic Emission?

A very common method used for electron emission is by heating the metal piece to a high temperature. The process of electron emission from the surface of metal into the surrounding space by heating the material is known as thermionic emission.

As the temperature of the metal piece rises, a point is reached at which some of the free electrons acquire sufficient velocity (or kinetic energy) to overcome the restraining surface forces and the electrons emit from the metal surface. The process of electron emission is similar to that of evaporation when liquid is heated i.e., the electrons seem to “boil off” the metal when its temperature is raised to a certain level. A surface that is used to provide flow of electrons by the thermionic emission is called a hot cathode.

The thermionic emission cannot readily take place in the air at normal atmospheric pressure. Moreover, the heated metal would tend to combine chemically with the oxygen of the air and might rapidly get destroyed at high operating temperature. Hence the thermionic emitters are heated either in evacuated space or in tubes filled with inert gases. Heat energy is usually supplied by passing the current through the emitter, which is made of high resistance wire of the required metal. For obtaining higher efficiency thermionic emitter is made of material with low work function so that material can be operated at low temperature.

The number of electrons ‘evaporated’ per unit area of an emitting surface depends upon the absolute temperature, T (Kelvins) of the emitter and thermionic work function for the particular combination of emitting surface and surrounding atmosphere, b. The emission current is given by the equation derived by O.W. Richardson, also known as Richardson Dushman equation, as below

where

• J_s is the emission current density in amperes/m²
• T is the temperature of surface in K
• A is a proportionality constant, also called the Plank’s constant, in amperes/m²/K²
• b is a constant of the emitter in Kelvin’s and
• e is the natural logarithmic base and equal to 2.7183.

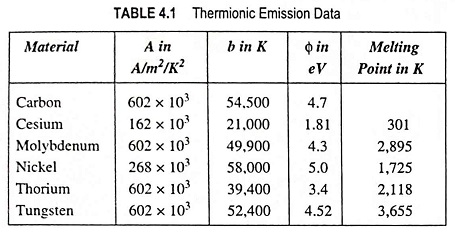
The value of A is the same for most pure metals (approximately 600,000) but varies widely for the practical emitters. The value of b remains constant for the metal and varies slightly with the temperature. The value of b is given by the equation

where

• Φ is the work function of the emitting surface in eV
• e is equal to electron charge i.e., 1.602 x 10^-19 coulomb and
• k′ is Boltzmann’s constant and is equal to 1.38 x 10^-23 J/K.

From the above equation, we see that in order to get large emission either the work function Φ must be low or the temperature T must be high. Also it is clear that if the work function can be halved by choosing suitable material, the absolute temperature can be halved without altering the value of the exponential factor.

A few approximate values of the constants for certain metals are given below in the tabular form.

The Dushman relation serves for design of thermionic devices and also points out a current limit imposed on their operation. This maximum current which can be obtained from thermal electron source at a given temperature is called the temperature saturation value.

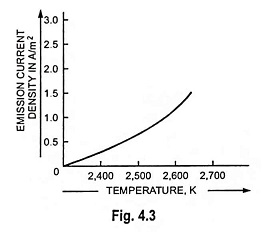
Electron tubes are operated in a fairly narrow temperature range-the lower limit be­ing fixed by sufficient emis­sion, and the upper limit by evaporation or melting of the emitter material. The curve showing the relation between the emission cur­rent density (amperes/m²) and temperature (K) for tungsten in its normal op­erating range is illustrated in Fig. 4.3.

The Schottky Effect:

The presence of electric field at the cathode surface reduces the work function Φ with a consequent increase in the thermionic emission to a small extent. In practical electronics this increase makes only quantitative difference as the full emission current is rarely drawn from the cathode. The Schottky effect is not to be confused with high field emission which needs much more intense electric field.