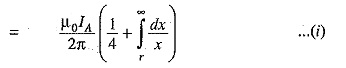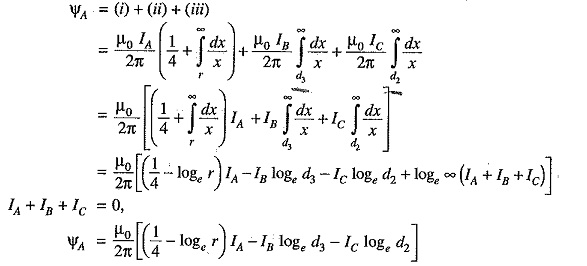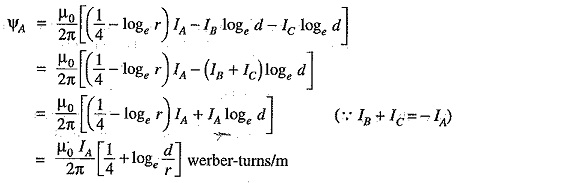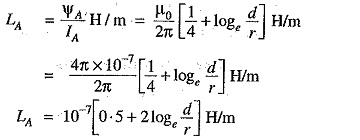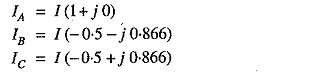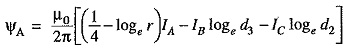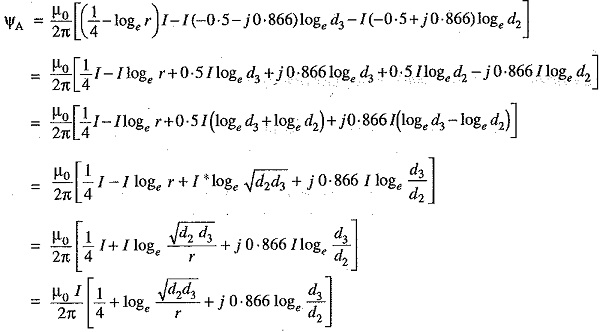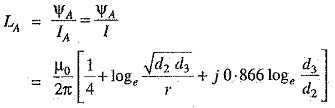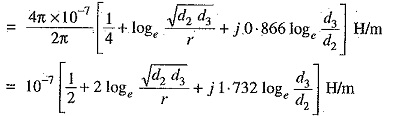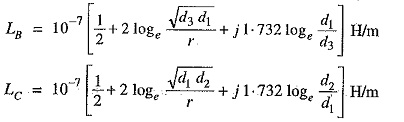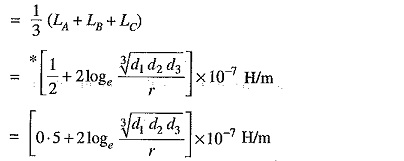Inductance of 3 Phase Overhead Line:

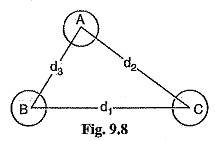
Fig. 9.8 shows the three conductors A, B and C of a Inductance of 3 Phase Overhead Line carrying currents I_A, I_B and I_C respectively. Let d₁, d₂ and d₃ be the spacings between the conductors as shown. Let us further assume that the loads are balanced i.e. I_A + I_B + I_C = 0. Consider the flux linkages with conductor A. There will be flux linkages with conductor A due to its own current and also due to the mutual inductance effects of I_B and I_C.

Flux linkages with conductor A due to its own current

Flux linkages with conductor A due to current I_B

Flux linkages with conductor A due to current I_C

Total flux linkages with conductor A is nr

1.Symmetrical spacing:

If the three conductors A, B and C are placed symmetrically at the corners of an equilateral triangle of side d, then, d₁ = d₂ = d₃ = d. Under such conditions, the flux linkages with conductor A become :

Inductance of conductor A,

Derived in a similar way, the expressions for inductance are the same for conductors B and C.

2.Unsymmetrical spacing:

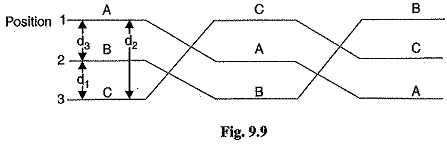
When 3-phase line conductors are not equidistant from each other, the conductor spacing is said to be unsymmetrical. Under such conditions, the flux linkages and Inductance of 3 Phase Overhead Line of each, phase are not the same. A different inductance in each phase results in unequal voltage drops in the three phases even if the currents in the conductors are balanced. Therefore, the voltage at the receiving end will not be the same for all phases. In order that voltage drops are equal in all conductors, we generally interchange the positions of the conductors at regular inter­vals along the line so that each conductor occupies the original position of every other conductor over an equal distance. such an exchange of positions is known as transposition. Fig. 9.9 shows the transposed line. The phase conductors are designated as A, B and C and the positions occupied are numbered 1, 2 and 3. The effect of transposition is that each conductor has the same average induc­tance.

Fig. 9.9 shows a 3-phase transposed line having unsymmetrical spacing. Let us assume that each of the three sections is 1 m in length. Let us further assume balanced conditions i.e., I_A + I_B + I_C = 0. Let the line currents be :

As proved above, the total flux linkages per metre length of conductor A is

Putting the values of I_A , I_B and I_C , we get,

Inductance of conductor A is

Similarly inductance of conductors B and C will be :

Inducance of each line conductor

If we compare the formula of inductance of an unsymmetrically spaced transposed line with that of symmetrically spaced line, we find that Inductance of 3 Phase Overhead Line of each line conductor in the two cases will be equal if d=∛d₁d₂d₃. The distance d is known as equivalent equilateral spacing for unsymmetrically transposed line.