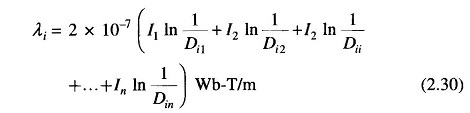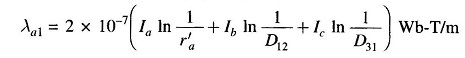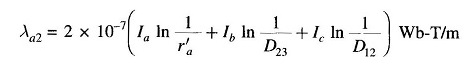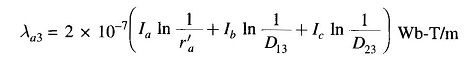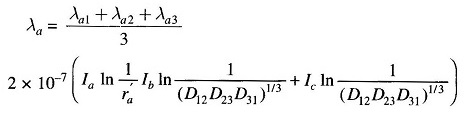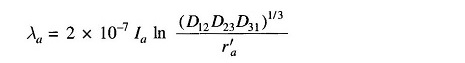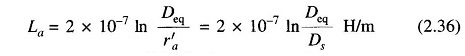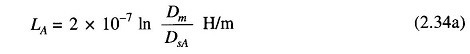Inductance of Three Phase Line with Unsymmetrical Spacing:
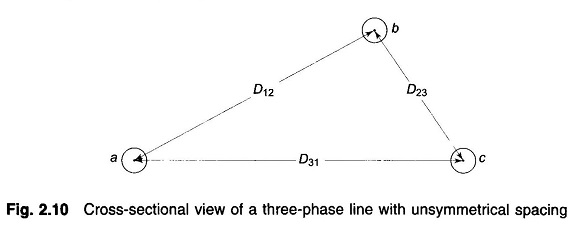
The basic equations developed can, however, be easily adapted to the calculation of the Inductance of three phase line. Figure 2.10 shows the conductors of a three phase line with unsymmetrical spacing.
Assume that there is no neutral wire, so that
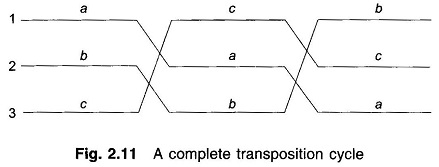
Unsymmetrical spacing causes the flux linkages and therefore the inductance of each phase to be different resulting in unbalanced receiving-end voltages even when sending-end voltages and line currents are balanced. Also voltages will be induced in adjacent communication lines even when line currents are balanced. This problem is tackled by exchanging the positions of the conductors at regular intervals along the line such that each conductor occupies the original position of every other conductor over an equal distance. Such an exchange of conductor positions is called transposition.
A complete transposition cycle is shown in Fig. 2.11. This arrangement causes each conductor to have the same average inductance over the transposition cycle. Over the length of one transposition cycle, the total flux linkages and hence net voltage induced in a nearby telephone line is zero.
To find the average inductance of each conductor of a transposed line, the flux linkages of the conductor are found for each position it occupies in the transposed cycle. Applying Eq. (2.30) to conductor a of Fig. 2.11, for section 1 of the transposition cycle wherein a is in position 1, b is in position 2 and c is in position 3, we get
For the second section
For the third section
Average flux linkages of conductor a are
But, Ib + Ic = -Ia, hence
Let
Then
This is the same relation as Eq. (2.34a)
where
- Dm = Deq, the mutual GMD between the three-phase conductors.
If ra = rb = rc, we have
It is not the present practice to transpose the power lines at regular intervals. However, an interchange in the position of the conductors is made at switching stations to balance the inductance of three phase line. For all practical purposes the dissymmetry can be neglected and the inductance of an untransposed line can be taken equal to that of a transposed line.
If the spacing is equilateral, then
and
If ra = rb = rc , it follows from Eq. (2.37) that