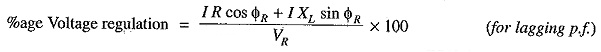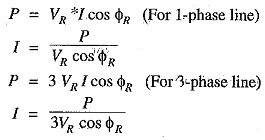Performance of Three Phase Short Transmission Line:

For reasons associated with economy, transmission of electric power is done by Three Phase Short Transmission Line. This system may be regarded as consisting of three single Phase units, each wire transmitting one-third of the total power. As a matter of convenience, we generally analyse 3-phase system by considering one phase only.

Therefore, expression for regulation, efficiency etc. derived for a single phase line can also be applied to a 3-phase system. Since only one phase is considered, phase values of Three Phase Short Transmission Line should be taken. Thus, V_S and V_R are the phase voltages, whereas R and X_L are the resistance and inductive reactance per phase respectiyely.

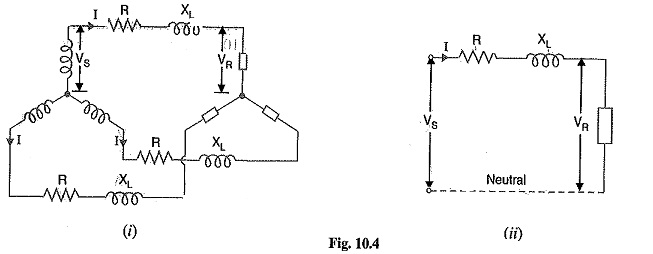
Fig. 10.4 (i) shows a Y-connected generator supplying a balanced Y-connected load through a transmission line. Each conductor has a resistance of R Ω and inductive reactance of X_LΩ. Fig. 10 4 (ii) shows one phase separately. The calculations can now be made in the same way as for a single phase line.

Effect of Load p.f. on Regulation and Efficiency

The regulation and efficiency of a transmission line depend to a considerable extent upon the power factor of the load.

1. Effect on regulation: The expression for voltage regulation of a short transmission line is given by

The following conclusions can be drawn from the above expressions

• When the load p.f. is lagging tir unity or such leading that I R cos Φ_R > I X_Lsin Φ_R, then voltage regulation is positive e., receiving end voltage V_R will be less than the sending end voltage V_S.
• For a given,V_R and I, the voltage regulation of the line increases with the decrease in p.f. for lagging loads.
• When the load p.f. is leading to this extent that I X_L sin Φ_R > I R cos Φ_R, then voltage regulation is negative i.e. the’receiving end voltage V_R is more than the sending end voltage V_S.
• For a V_R and I, the voltage regulation of the line decrease with the decrease in p.f. for leading loads.

2. Effect on transmission efficiency: The power delivered to the load depends upon the power factor.

It is clear that in each case, for a given amount of power to be transmitted (P) and receiving end voltage (V_R), the load current I is inversely proportional to the load p.f. cos Φ_R. Consequently, with the decrease in load p.f., the load current and hence the line losses are increased. This leads to the conclusion that transmission efficiency of a line decreases with the decrease in load p.f. and vice-versa.